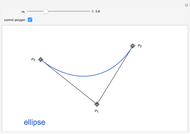
Subdivision Algorithm for Bézier Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
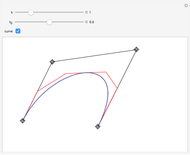
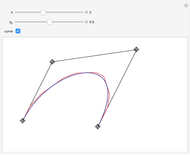
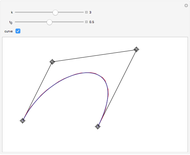
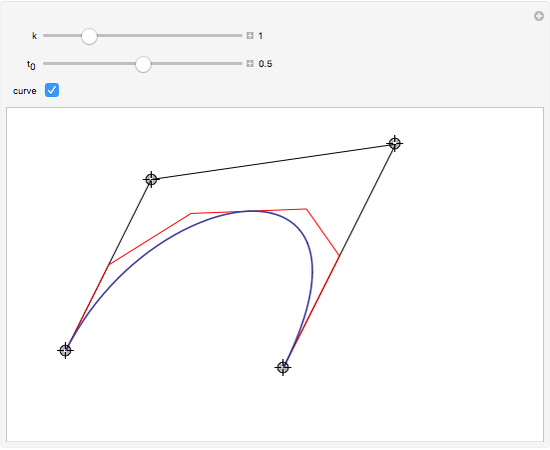
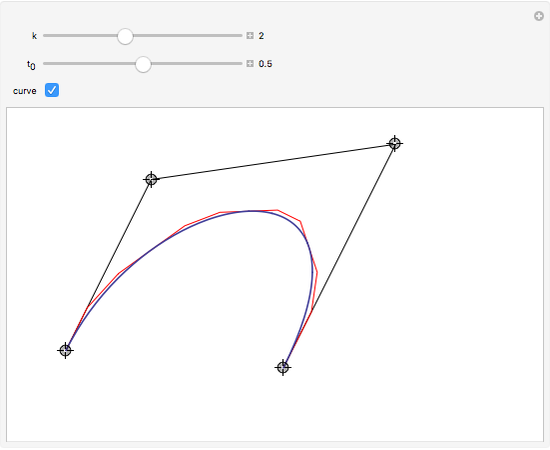
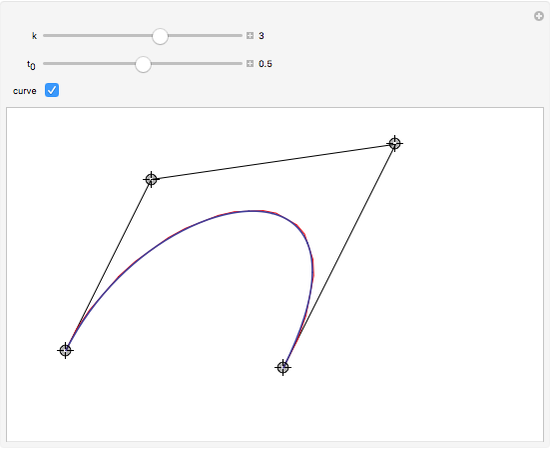
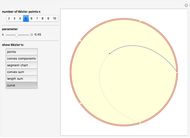
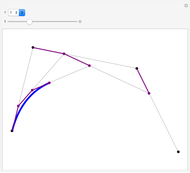
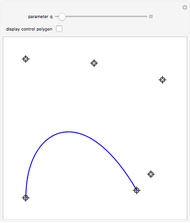
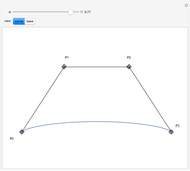
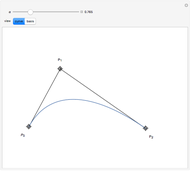
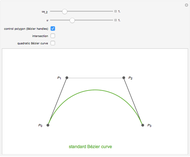
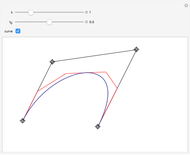
This Demonstration illustrates the convergence of the de Casteljau-based subdivision algorithm for Bézier curves.
Contributed by: Isabelle Cattiaux-Huillard (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
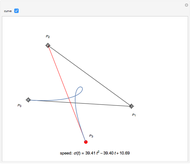
The subdivision algorithm follows from the de Casteljau algorithm that calculates a current point 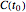 , for
, for 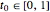 , of a polynomial Bézier curve
, of a polynomial Bézier curve 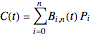 , for
, for 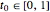 , where
, where  are the control points, by applying the following recurrence formula:
are the control points, by applying the following recurrence formula:
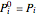 for
for 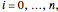
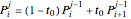 for
for 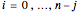 .
.
For any value of 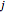 between
between  and
and  , we have
, we have
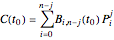 .
.
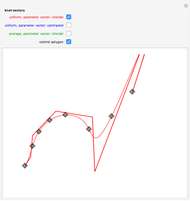
The subdivision algorithm associates to the polygon 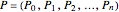 the two polygons
the two polygons 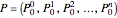 and
and 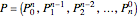 . They constitute the control polygons of the two parts of the curve
. They constitute the control polygons of the two parts of the curve 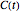 , respectively for
, respectively for  in
in 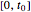 and
and 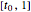 :
:
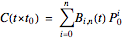
and
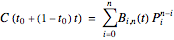 .
.
When 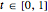 ,
, 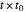 varies over
varies over 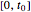 and
and 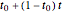 varies over
varies over 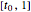 .
.
This Demonstration illustrates repeated application of the above procedure (the control "k" denotes the number of iterations). Obviously, the resulting polygon sequence converges very quickly to the curve 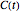 .
.
Permanent Citation