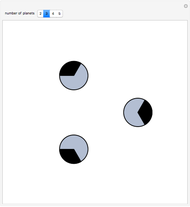
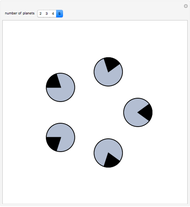
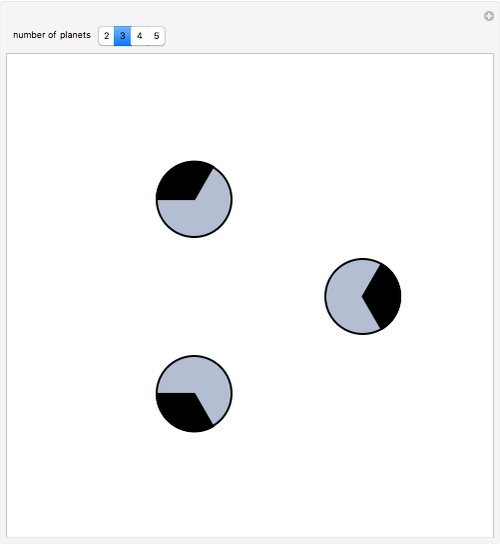
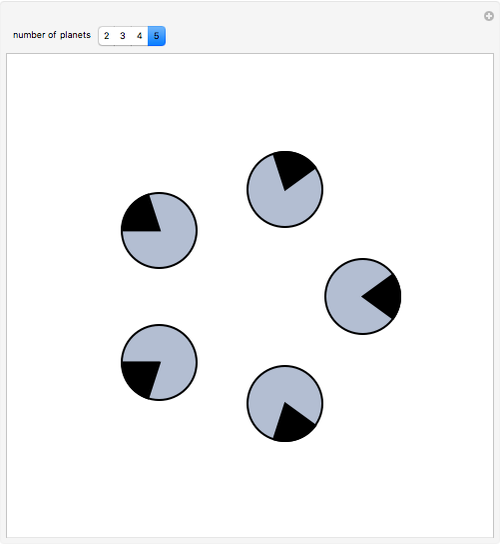
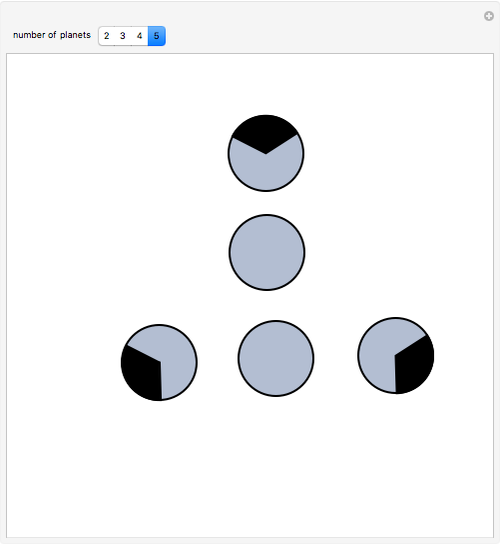
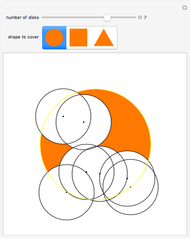
Consider a set of circular planets in the plane (disks), all of the same radius and no two intersecting. On the circumference of each planet, look at the set of points not visible from any other planet (indicated by a dark sector). Incredibly, the total length of these sets is equal to the circumference of one planet! This problem was in the short list of the 22nd International Mathematical Olympiad, proposed by the Soviet Union. You can drag the disks to see the set of shadows they impose on one another.