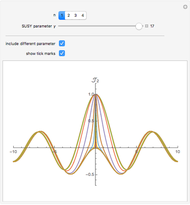
Supersymmetric Partner Bessel Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
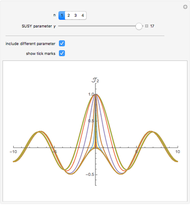
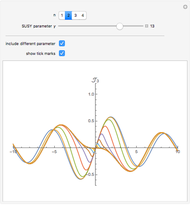
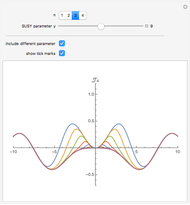
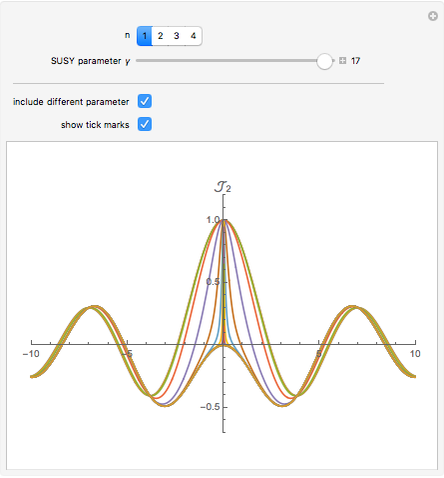
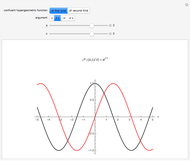
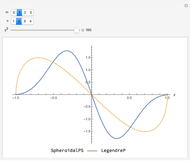
The partner Bessel functions are given by 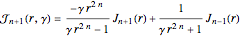 . The supersymmetry (SUSY) parameter
. The supersymmetry (SUSY) parameter 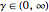 determines the transition beween Bessel functions of different order, from
determines the transition beween Bessel functions of different order, from  to
to  for arbitrary
for arbitrary  .
.
Contributed by: N. Barbosa-Cendejas, and M. A. Reyes (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The partner Bessel equation
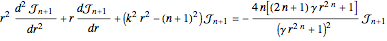
is derived from a supersymmetric (SUSY) type of factorization of Bessel's equation, which also applies to other Sturm–Liouville equations. The partner Bessel functions  show an interesting and unusual SUSY behavior: the SUSY parameter γ links these functions to a pair of Bessel functions differing by two orders
show an interesting and unusual SUSY behavior: the SUSY parameter γ links these functions to a pair of Bessel functions differing by two orders
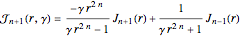 .
.
Since 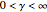 , this SUSY parameter takes the partner Bessel functions from
, this SUSY parameter takes the partner Bessel functions from 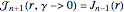 to
to 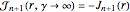 .
.
In the snapshots you can see the shape of the partner Bessel functions as they evolve from one order to another for different values of the SUSY parameter.
References:
[1] N. Barbosa-Cendejas and M. A. Reyes, "Damped Wave Equation from Isospectral Bessel Functions," Rev. Mex. Fís., 54, 2008 pp. 319–321. [2] M. A. Reyes, D. Jimenez, and H. C. Rosu, "One-Parameter Isospectral Special Functions," Rev. Mex. Fís., 49, 2003 pp. 358–363.
Permanent Citation