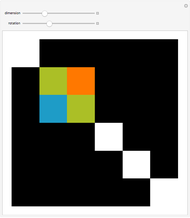
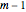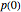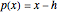Sylvester Matrix
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
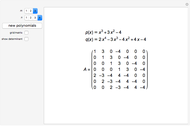
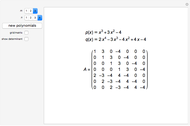
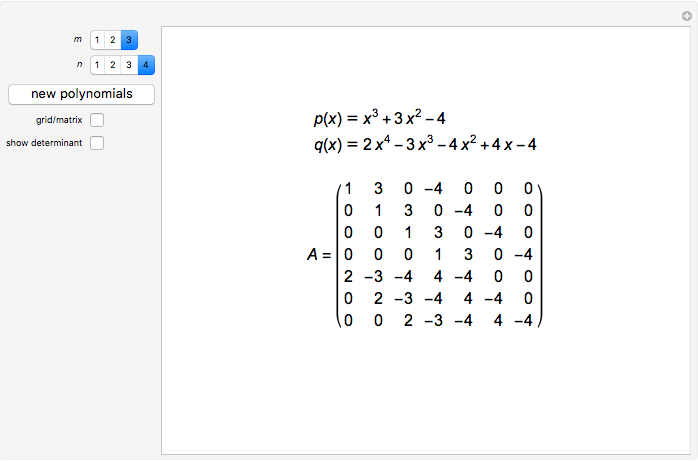
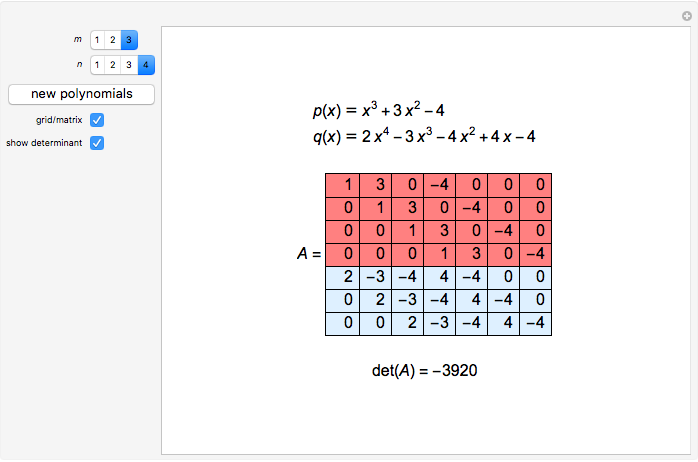
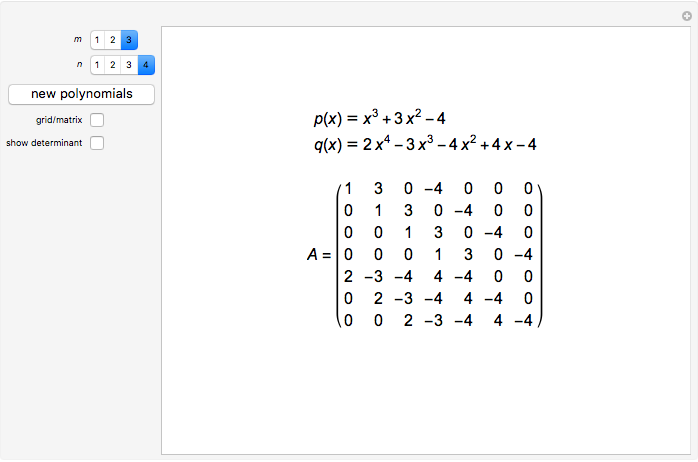
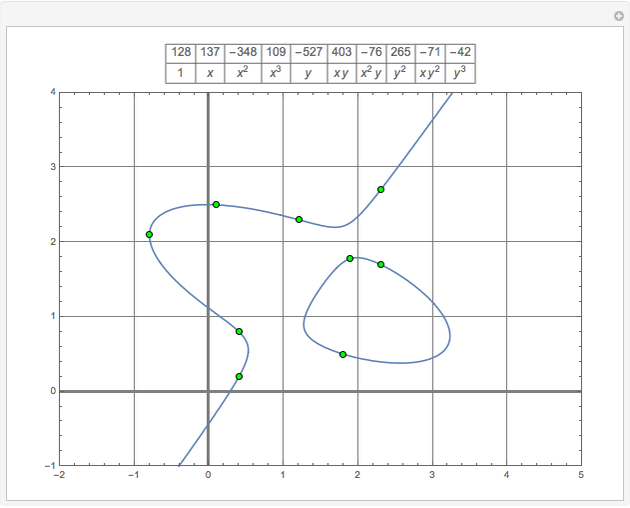
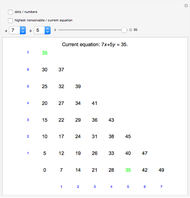
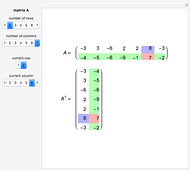
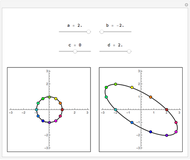
This Demonstration shows the 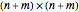 Sylvester matrix of two polynomials
Sylvester matrix of two polynomials 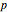 and
and  of positive degrees
of positive degrees 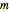 and
and  .
.
Contributed by: Izidor Hafner (December 2016)
Open content licensed under CC BY-NC-SA
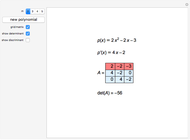
Snapshots
Details
Reference
[1] D. Kurepa, High Algebra, Book 1 (in Croatian), Zagreb: Skolska knjiga, 1965.
Permanent Citation