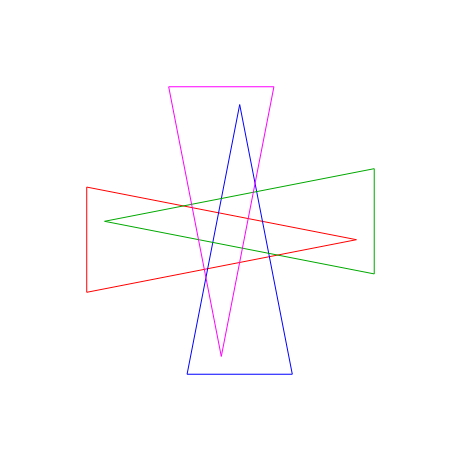
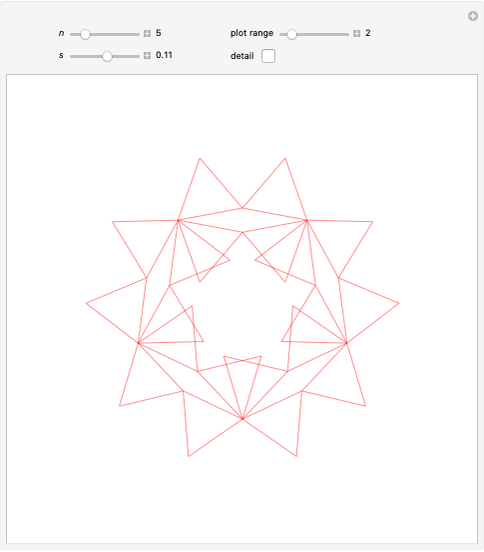
Symmetric Independent Families of Four Isosceles Triangles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
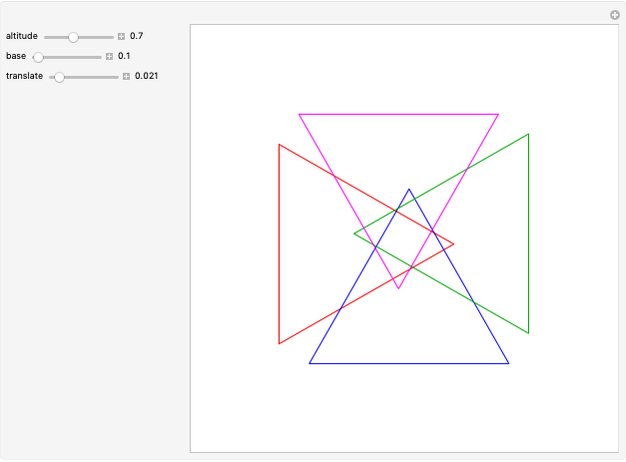
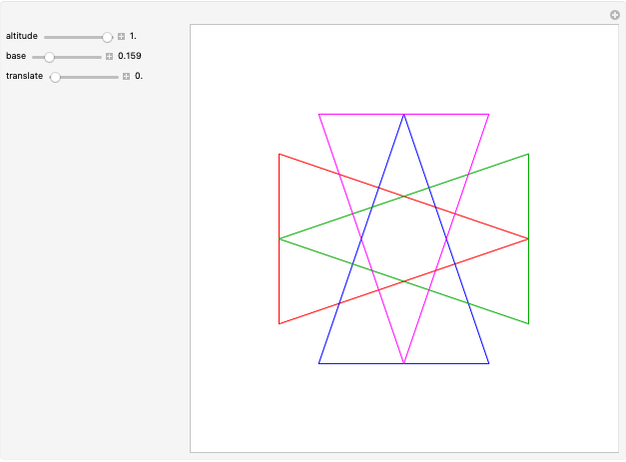
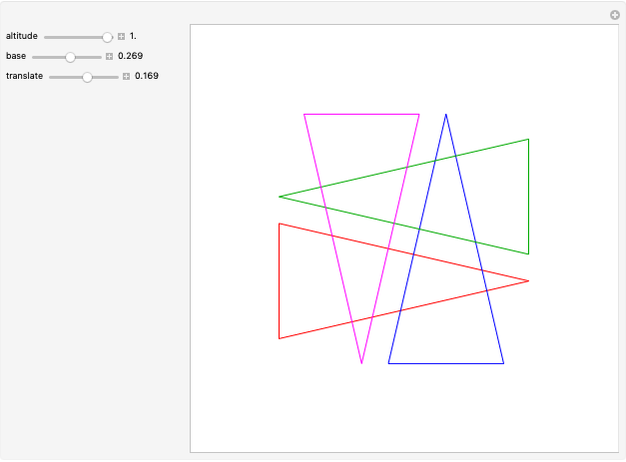
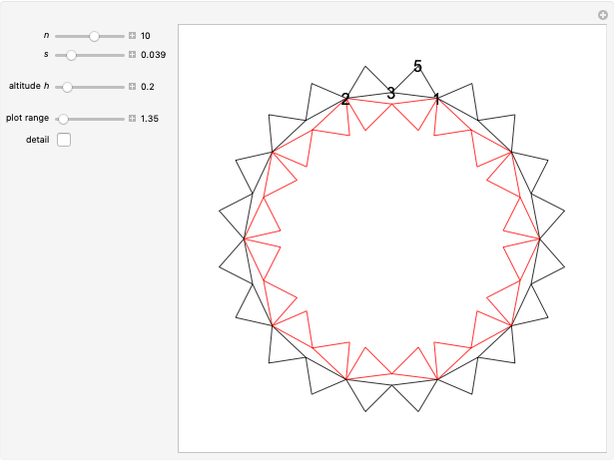
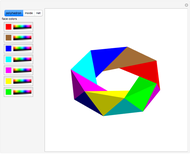
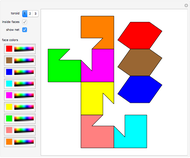
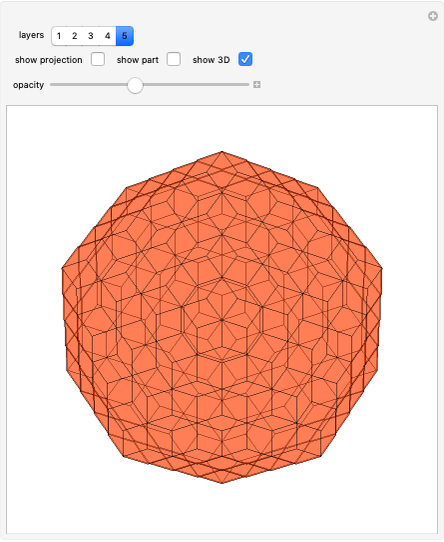
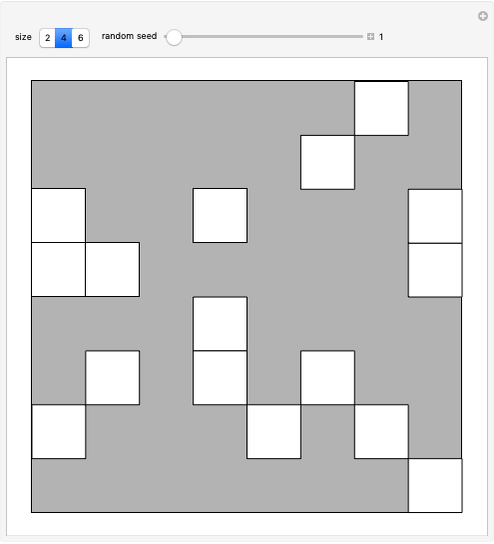
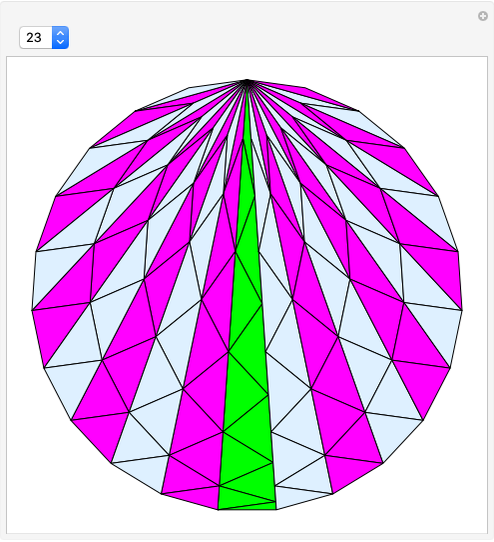
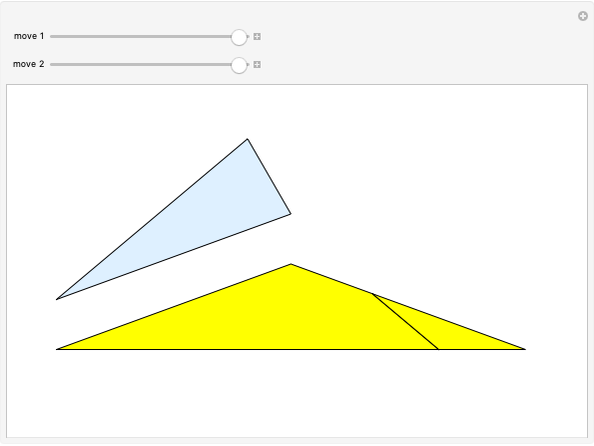
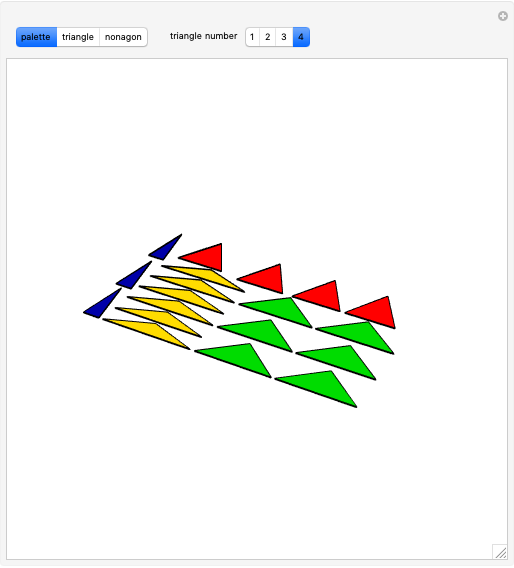
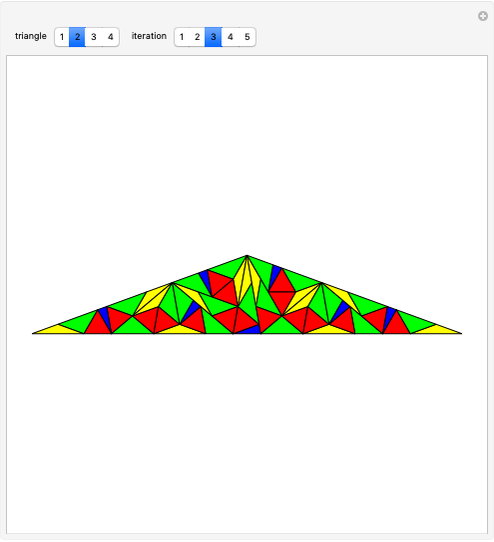
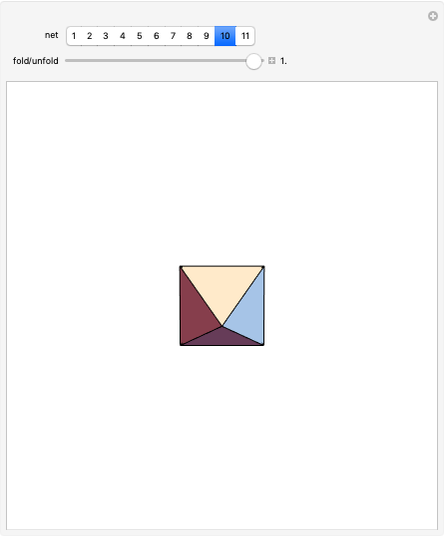
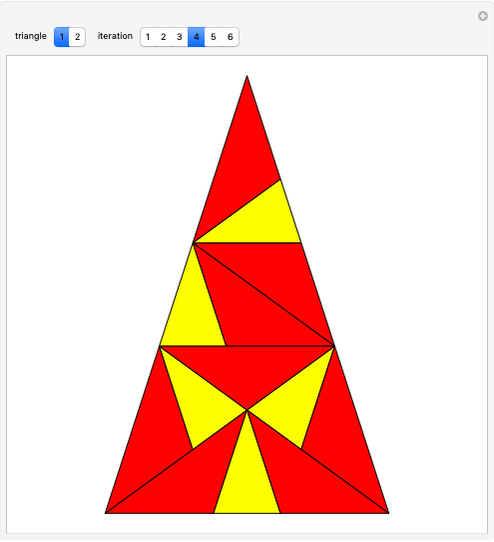
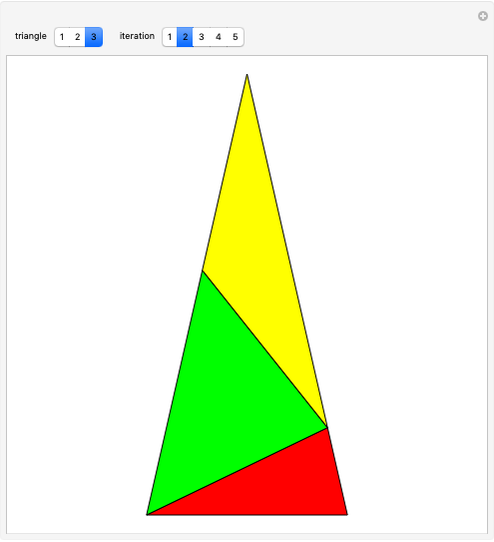
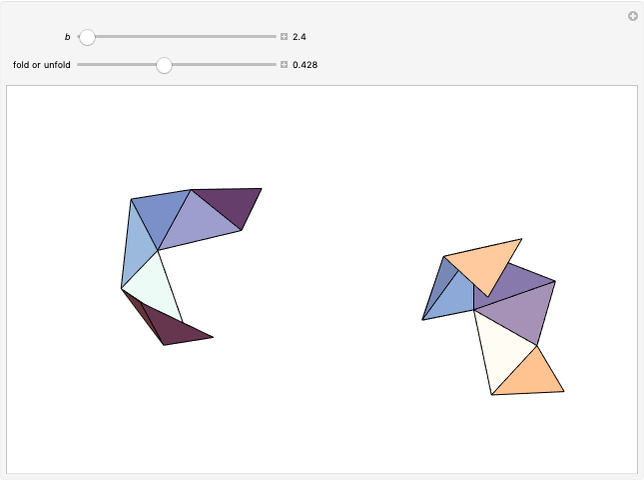
This Demonstration shows symmetric independent families of four isosceles triangles with up to 18 regions.
Contributed by: Izidor Hafner (April 2019)
Open content licensed under CC BY-NC-SA
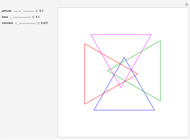
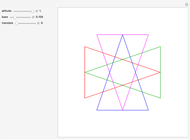
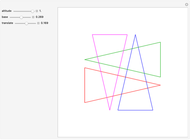
Snapshots
Details
Consider a family  of
of  simple (Jordan) curves that intersect pairwise in finitely many points. Let
simple (Jordan) curves that intersect pairwise in finitely many points. Let  be either the interior or the exterior of
be either the interior or the exterior of  . The family is called independent if
. The family is called independent if

for each of the 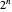 possible choices of the
possible choices of the 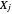 . If, moreover, each of the sets
. If, moreover, each of the sets  is connected, the independent family
is connected, the independent family  is called a Venn diagram. An independent family or Venn diagram is called simple if no three curves have a common point [1, p. 104].
is called a Venn diagram. An independent family or Venn diagram is called simple if no three curves have a common point [1, p. 104].
An example with equilateral triangles is from [1, p. 107].
Reference
[1] B. Grünbaum, "The Search for Symmetric Venn Diagrams," Geombinatorics, 8(4), 1999 pp. 104–109. (Apr 4, 2019) sites.math.washington.edu/~grunbaum/SymmetricVennDiagrams.pdf.
Permanent Citation