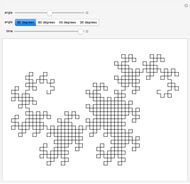
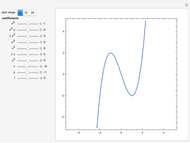
Symmetry of a Mystery Curve

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
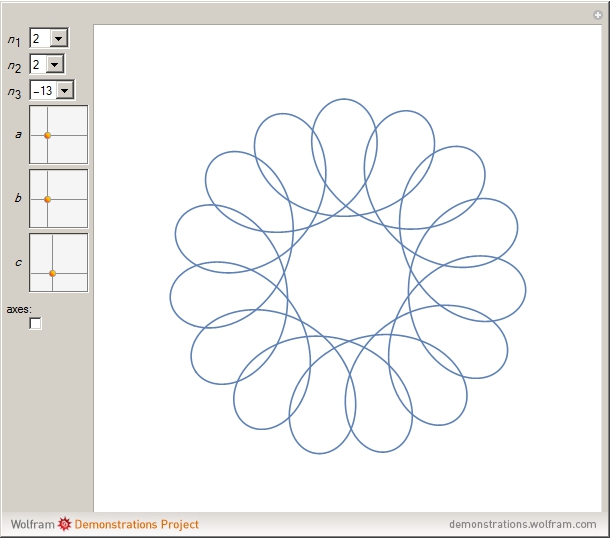
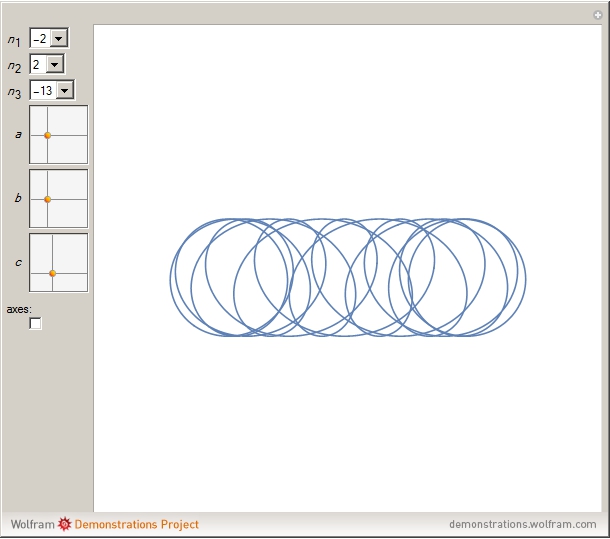
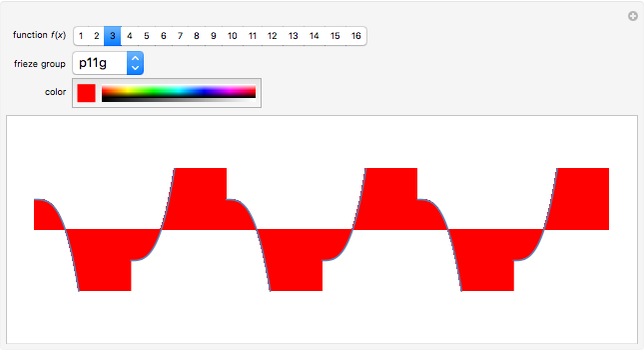
This Demonstration shows graphs of the function  , where
, where  ,
,  , and
, and  are complex coefficients and the frequencies
are complex coefficients and the frequencies  ,
, 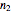 , and
, and  are integers. In particular, for the frequencies 1, 6, and -14, the curve has five-fold symmetry.
are integers. In particular, for the frequencies 1, 6, and -14, the curve has five-fold symmetry.
Contributed by: Izidor Hafner (January 2016)
(Based on the work of Frank A. Farris)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The following theorem is shown [1, pp. 13]:
Suppose that 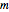 and
and  are integers and that all the frequency numbers
are integers and that all the frequency numbers 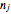 in the finite sum
in the finite sum
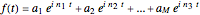
satisfy  .
.
Then, for any choice of the coefficients  ,
, 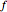 satisfies the symmetry condition
satisfies the symmetry condition
 for all
for all  .
.
Reference
[1] F. A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015.
Permanent Citation