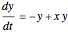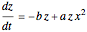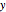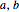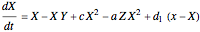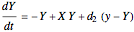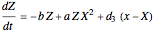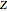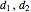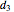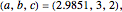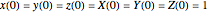Synchronization of Chaotic Attractors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
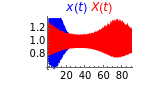
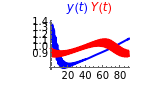
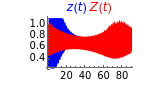
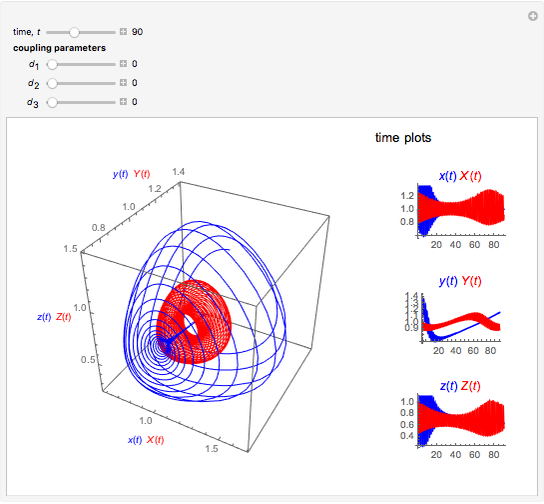
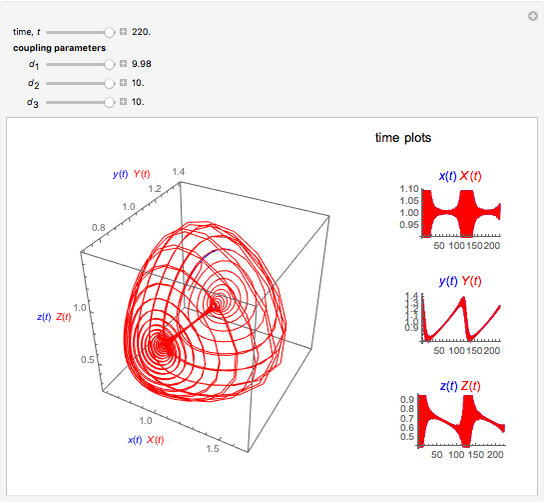
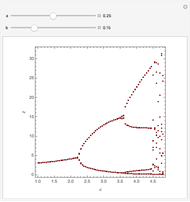
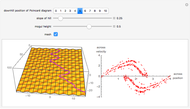
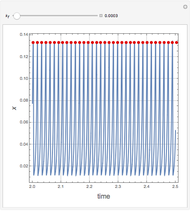
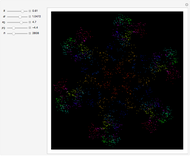
This Demonstration illustrates a method for synchronizing the trajectories of two modified Lotka–Volterra systems. Synchronization is accomplished by linear feedback [1], with the governing equations of the first system [2] as follows:
[more]
Contributed by: Clay Gruesbeck (August 2013)
Open content licensed under CC BY-NC-SA
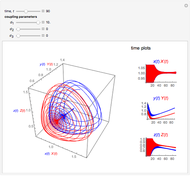
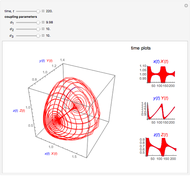
Snapshots
Details
References
[1] T. Kapitaniak, Controlling Chaos: Theoretical and Practical Methods in Non-linear Dynamics, San Diego: Academic Press, 1996.
[2] J. S. Costello, "Synchronization of Chaos in a Generalized Lotka–Volterra Attractor," The Nonlinear Journal, 1, 1999 pp. 11–17.
Permanent Citation