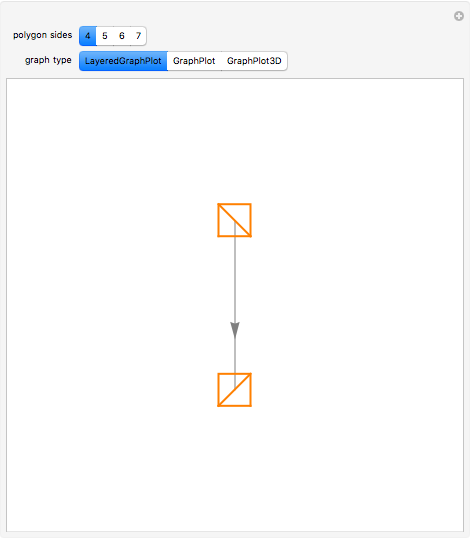
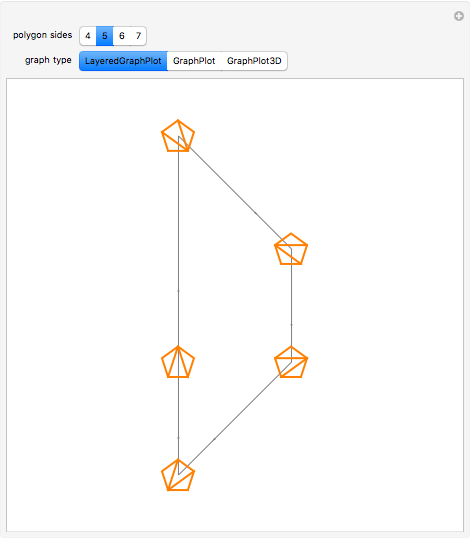
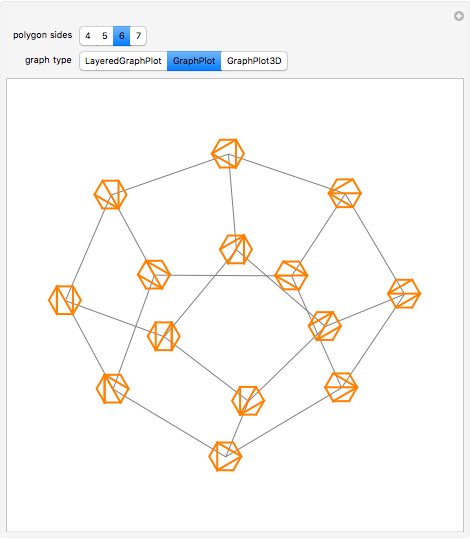
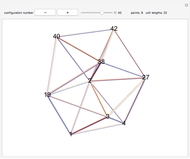
Tamari Lattice

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
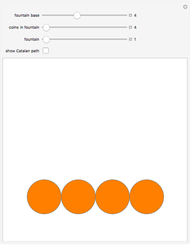
There are multiple ways to parenthesize a sequence of factors two at a time. For instance,  ,
,  , and
, and  can be grouped as either
can be grouped as either 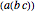 or
or 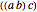 ; the Catalan numbers count the number of ways this is possible for
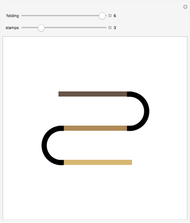
; the Catalan numbers count the number of ways this is possible for  factors. The groupings form a partially ordered set, where one grouping covers another if the first can be transformed into the second by taking a subelement of the form
factors. The groupings form a partially ordered set, where one grouping covers another if the first can be transformed into the second by taking a subelement of the form 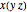 and replacing it with
and replacing it with 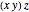 . In these transformations,
. In these transformations,  ,
,  , and
, and  can be a single factor or a product of factors. These partially ordered sets form a lattice called the Tamari lattice.
can be a single factor or a product of factors. These partially ordered sets form a lattice called the Tamari lattice.
Contributed by: Robert Dickau (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
R. P. Stanley, Enumerative Combinatorics, Volume 2, Cambridge: Cambridge University Press, 1999 pp. 234–235.
Permanent Citation
"Tamari Lattice"
http://demonstrations.wolfram.com/TamariLattice/
Wolfram Demonstrations Project
Published: March 7 2011