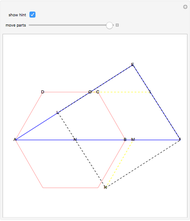
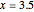Tarski's Adaptation of Wojtowicz's Argument on Optimal Dissection of a Unit Square

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
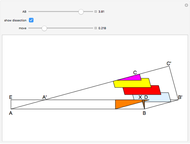
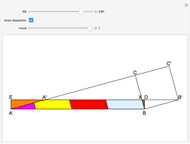
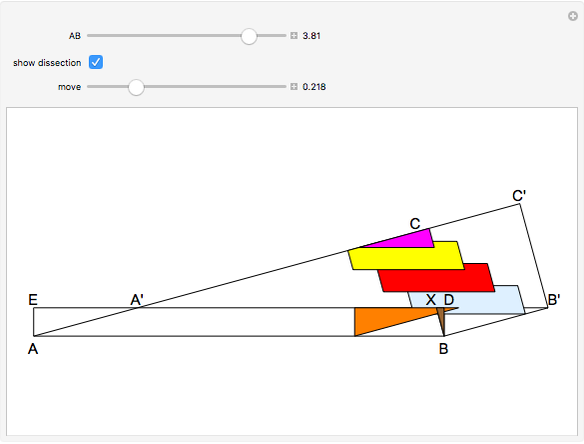
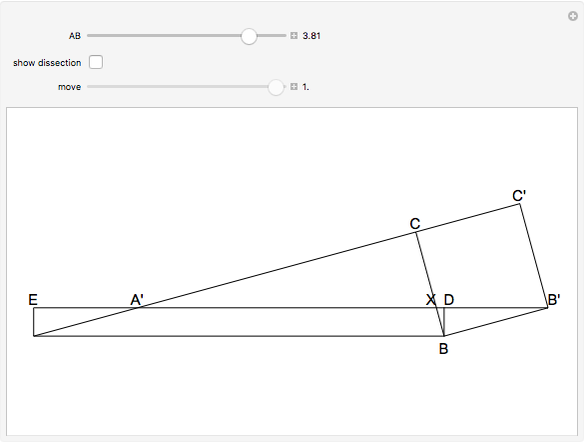
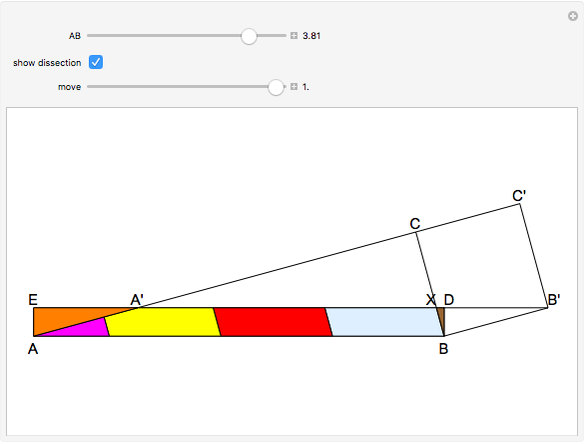
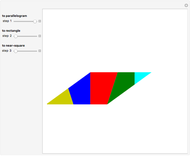
This Demonstration shows a reconstruction of a theorem of Tarski. An optimal dissection uses the smallest number of pieces. The theorem states that the number of pieces in an optimal dissection of a unit square into a rectangle of dimensions  and
and 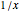 has an upper bound
has an upper bound 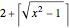 , where
, where 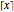 denotes the ceiling of
denotes the ceiling of  , that is, the smallest integer greater than or equal to
, that is, the smallest integer greater than or equal to  .
.
Contributed by: Izidor Hafner (May 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Before World War II, the famous logician Alfred Tarski worked as a high school teacher and as assistant to Jan Łukasiewicz. His contributions to elementary mathematics are described in [1].
Polygons that have the same area are called equivalent. In the article "On the Degree of Equivalence of Polygons," Tarski defines the degree of equivalence of two equivalent polygons 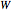 and
and 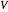 as the smallest natural number
as the smallest natural number  for which there exists an
for which there exists an  -piece dissection of
-piece dissection of 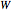 to
to 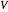 . The function is denoted as
. The function is denoted as 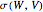 .
.
If 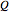 is a square of side
is a square of side  and
and 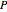 is a rectangle of sides
is a rectangle of sides 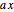 and
and 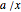 , Tarski introduces
, Tarski introduces 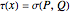 and states a theorem about the function
and states a theorem about the function  .
.
Tarski did not prove the theorem, but he gave some hints with reference to Wojtowich's book for high schools. The theorem of this Demonstration has been proved using Mathematica graphics [1, pp. 128, 129].
Reference
[1] A. McFarland, J. McFarland and J. T. Smith, eds., Alfred Tarski: Early Work in Poland: Geometry and Teaching, New York: Birkhäuser, 2014.
Permanent Citation