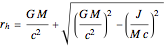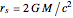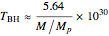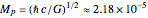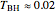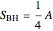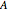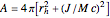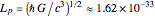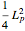Temperature and Entropy of a Black Hole

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
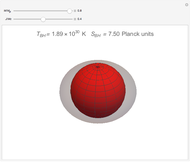
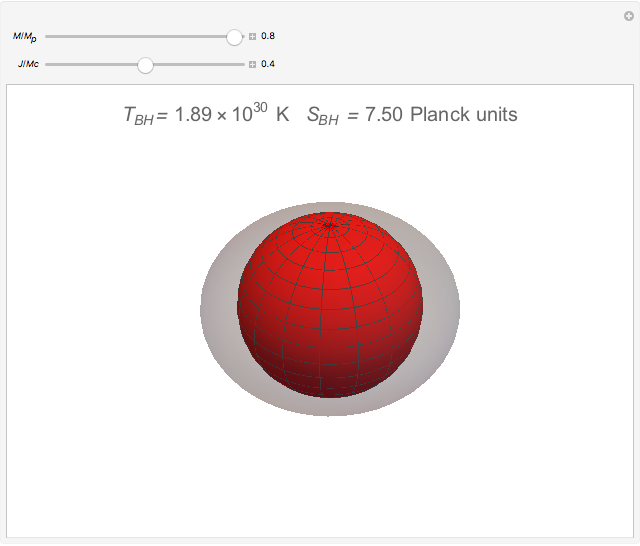
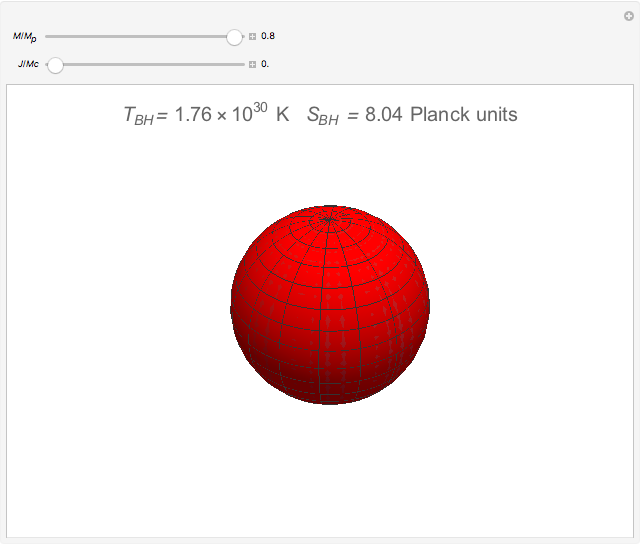
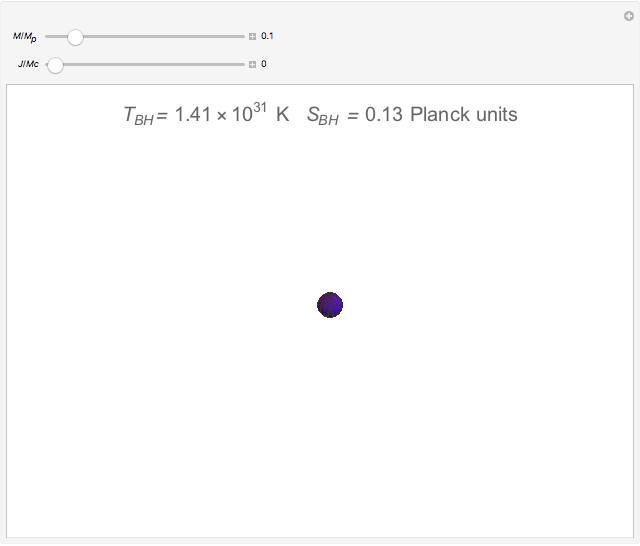
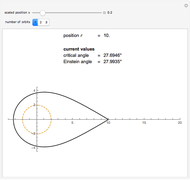
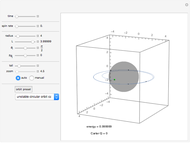
According to the "no hair theorems" of general relativity, the properties of an electrovac black hole (i.e., a black hole whose exterior is a vacuum and whose interior contains electromagnetic but no other charges) are completely determined by just three parameters: mass 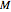 , angular momentum
, angular momentum  , and electric (or magnetic monopole) charge
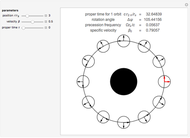
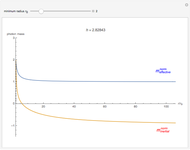
, and electric (or magnetic monopole) charge 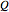 . While this suggests a possible violation of the second law of thermodynamics, since the entropy of the universe could be reduced by creating single-microstate black holes, the black hole region is classically experimentally inaccessible. Thus, it is possible that a quantum mechanical black hole can possess additional microstates. Moreover, in a series of papers starting in 1973, Jacob Bekenstein showed that the area of a black hole seemed to be a measure of the entropy of a black hole, in precisely the correct magnitude to preserve the second law. In 1974, Stephen Hawking proposed, based on quantum field theory (QFT), that the immense energy density of a black hole's gravitational field could give rise to continual creation and annihilation of virtual particles and antiparticles, with lifetimes consistent with the uncertainty principle,
. While this suggests a possible violation of the second law of thermodynamics, since the entropy of the universe could be reduced by creating single-microstate black holes, the black hole region is classically experimentally inaccessible. Thus, it is possible that a quantum mechanical black hole can possess additional microstates. Moreover, in a series of papers starting in 1973, Jacob Bekenstein showed that the area of a black hole seemed to be a measure of the entropy of a black hole, in precisely the correct magnitude to preserve the second law. In 1974, Stephen Hawking proposed, based on quantum field theory (QFT), that the immense energy density of a black hole's gravitational field could give rise to continual creation and annihilation of virtual particles and antiparticles, with lifetimes consistent with the uncertainty principle,  . Should one of the virtual pair be swallowed up by the black hole, its partner would become a real particle which, to an outside observer, would appear to have been radiated by the black hole. Moreover, the effective temperature of the black hole corresponded nicely with Bekenstein's classical derivation, giving a physical justification for the earlier ad-hoc identification.
. Should one of the virtual pair be swallowed up by the black hole, its partner would become a real particle which, to an outside observer, would appear to have been radiated by the black hole. Moreover, the effective temperature of the black hole corresponded nicely with Bekenstein's classical derivation, giving a physical justification for the earlier ad-hoc identification.
Contributed by: Itai Seggev and S. M. Blinder (January 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] Wikipedia. "Black Hole." (Dec 19, 2011) en.wikipedia.org/wiki/Black_hole
[2] Wikipedia. "Black Hole Thermodynamics." (Dec 19, 2011) en.wikipedia.org/wiki/Thermodynamics_of_black _holes
Permanent Citation