Temperature-Dependent Rotational Energy Spectrum

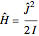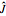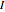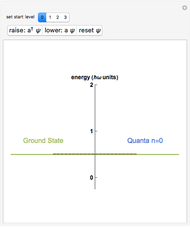
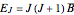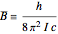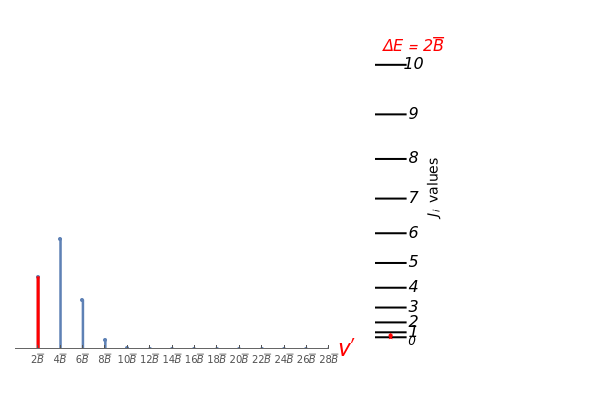
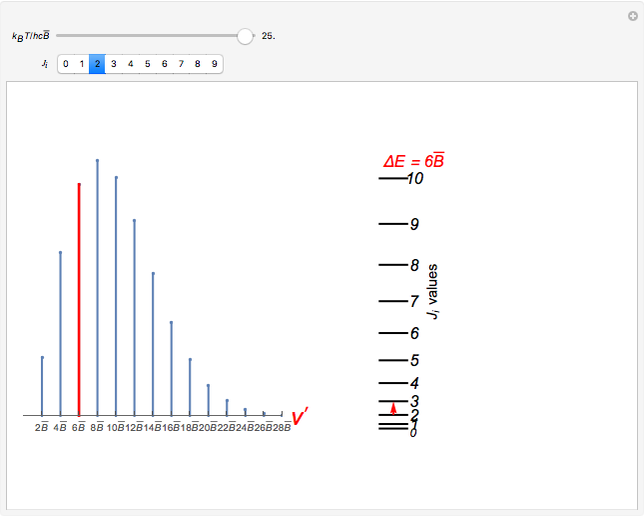
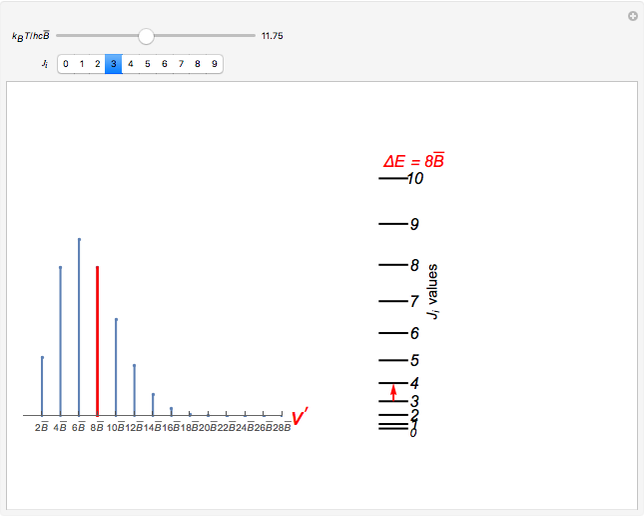
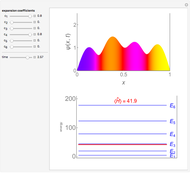
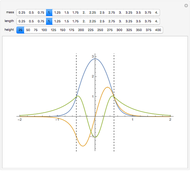
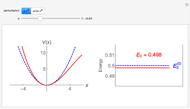
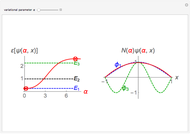
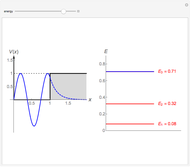
This Demonstration studies the pure rotational spectrum of the quantum rigid rotor problem (neglecting centrifugal distortion), described by the Hamiltonian , where is the angular momentum operator and is the moment of inertia. The energy levels are given by , where is the rotational constant and the transition frequency between two adjacent levels is (selection rules only allow transitions that satisfy ). The left graphic shows the spectrum consisting of a series of equally spaced lines, where the relative intensity of each line depends on the probability to occupy the initial state in thermal equilibrium, 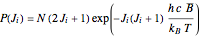, where is the Boltzmann constant and 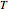is the temperature. The left and right graphics show the spectrum for a given ratio 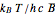and the energy level diagram, and the red highlighting shows the correspondence between a pair of energy levels and a specific transition frequency.