Testing an Intuitive Random Generator with the Task of Emptying a Cube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
It is to be expected that the less significant digits of 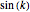 depend on the integer argument
depend on the integer argument  in a chaotic manner so that the formula
in a chaotic manner so that the formula 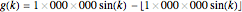 (where
(where 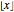 is the floor of
is the floor of  ) is expected to define a uniformly distributed sequence in the unit interval
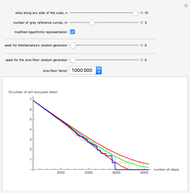
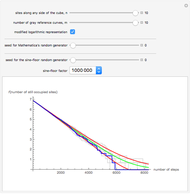
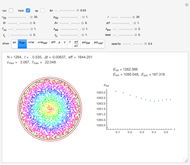
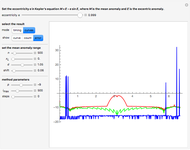
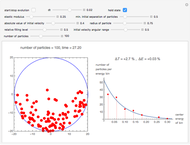
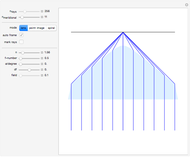
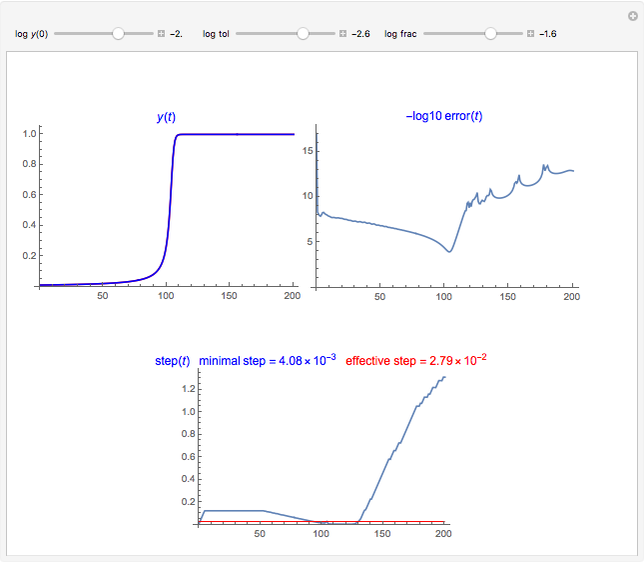
) is expected to define a uniformly distributed sequence in the unit interval  . This Demonstration lets you use this formula as a random generator and perform a rather selective test with it. We compute an entity (the blue curve) that—under the assumption that the random generator is perfect—is a realization of a certain stochastic process: emptying a cube. All properties of this process can be computed exactly and are shown by the green curve (decay of the "mean occupation number") and the two red curves (mean occupation number ± one standard deviation). The random generator passes the test if the blue curve remains approximately between the red lines.
. This Demonstration lets you use this formula as a random generator and perform a rather selective test with it. We compute an entity (the blue curve) that—under the assumption that the random generator is perfect—is a realization of a certain stochastic process: emptying a cube. All properties of this process can be computed exactly and are shown by the green curve (decay of the "mean occupation number") and the two red curves (mean occupation number ± one standard deviation). The random generator passes the test if the blue curve remains approximately between the red lines.
Contributed by: Ulrich Mutze (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The stochastic process under consideration is as follows: the basic object is the finite set 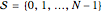 of sites, where
of sites, where 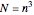 for some positive integer
for some positive integer  . The state space of the process is the powerset
. The state space of the process is the powerset 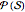 , and the initial state is
, and the initial state is 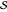 (
(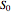 ), where
), where 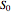 is the state for which every site is occupied. The allowed state transitions are in one-to-one correspondence with the sites. They are of the form
is the state for which every site is occupied. The allowed state transitions are in one-to-one correspondence with the sites. They are of the form  , that is, they just remove
, that is, they just remove  from the set
from the set 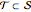 . Of course, this emptying of site
. Of course, this emptying of site  is the trivial action for states that do not contain
is the trivial action for states that do not contain  (states for which site
(states for which site  is empty). The stochastics of the process is defined by stipulating that state transitions (steps) occur in a fixed time raster and with equal probability for all transitions. The cardinality
is empty). The stochastics of the process is defined by stipulating that state transitions (steps) occur in a fixed time raster and with equal probability for all transitions. The cardinality 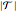 of a state
of a state 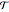 is referred to as its population size. Obviously the first step reduces the population size from
is referred to as its population size. Obviously the first step reduces the population size from  to
to 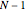 . The smaller the population becomes in a sequence of steps, the smaller the probability that the next step will reduce the population even more: the sites proposed for emptying may be empty already. This stochastic law is simple enough that all pertinent problems can be worked out analytically. The most important property is that the expectation value of the population size after
. The smaller the population becomes in a sequence of steps, the smaller the probability that the next step will reduce the population even more: the sites proposed for emptying may be empty already. This stochastic law is simple enough that all pertinent problems can be worked out analytically. The most important property is that the expectation value of the population size after 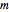 steps is
steps is 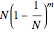 . A realization of the stochastic process asks for actually deciding which site should be selected for emptying in all the steps under consideration. As in all modern applications of the Monte Carlo method, this is done by calling a random number generator. If this function is set up to return integer numbers in the range
. A realization of the stochastic process asks for actually deciding which site should be selected for emptying in all the steps under consideration. As in all modern applications of the Monte Carlo method, this is done by calling a random number generator. If this function is set up to return integer numbers in the range 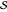 it can be directly used for this decision. Any realization of the process gives a curve representing the actual population sizes as they decrease with growing step number. The behavior of this curve can be compared with that of the mean value curve as given above. If there is a significant discrepancy between the mean value and the particular realization, we may have to blame the random generator for failing to give all its outputs with equal probability. Such a failure is very unlikely, however, for any reasonably designed random generator, and so we make the test more selective by making it sensitive for statistical dependencies of successive results: for realizing one step we call three times in succession a random number generator that returns numbers in the smaller set
it can be directly used for this decision. Any realization of the process gives a curve representing the actual population sizes as they decrease with growing step number. The behavior of this curve can be compared with that of the mean value curve as given above. If there is a significant discrepancy between the mean value and the particular realization, we may have to blame the random generator for failing to give all its outputs with equal probability. Such a failure is very unlikely, however, for any reasonably designed random generator, and so we make the test more selective by making it sensitive for statistical dependencies of successive results: for realizing one step we call three times in succession a random number generator that returns numbers in the smaller set 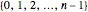 . Let
. Let  be the triplet of numbers obtained in this way. The site proposed for emptying, then, is
be the triplet of numbers obtained in this way. The site proposed for emptying, then, is 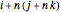 . This procedure suggests itself if we consider the sites as arranged in a finite cubic lattice and let the random generator output three discrete Cartesian coordinates of the site to be selected. The "name emptying a cube" refers to this situation [1].
. This procedure suggests itself if we consider the sites as arranged in a finite cubic lattice and let the random generator output three discrete Cartesian coordinates of the site to be selected. The "name emptying a cube" refers to this situation [1].
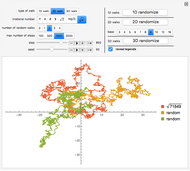
Snapshot 1: the blue curve remains within its expected limits; test passed, but only for a small number (1000) of points
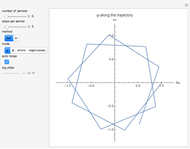
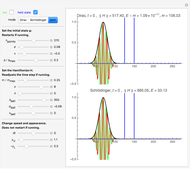
Snapshot 2: the gray curves carry essentially the same information as the green and red lines. Whereas the gray curves can always be obtained by the Monte-Carlo method, the red and green curves can only be obtained by analytical methods. For the present simple process, these are in place, however. The blue curve remains always within the area spanned by the 10 gray curves. Thus, there is no reason to blame the sine-floor random generator.
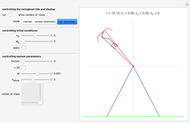
Snapshot 3: the sine-floor generator does not work properly if its factor is reduced from its proven value 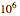 too drastically (modified logarithmic representation)
too drastically (modified logarithmic representation)
Snapshot 4: settings as for Snapshot 3, but non-logarithmic representation
[1] D. Stauffer, "Random Number Generation," Computational Physics (K. H. Hoffmann and M. Schreiber, eds.), New York: Springer, 1996.
[2] U. Mutze, "Rigidly Connected Overlapping Spherical Particles: A Versatile Grain Model," Granular Matter, 8(3–4), 2006 pp. 185–194.
[3] U. Mutze, "Polyspherical Grains and Their Dynamics," 2007.
Permanent Citation