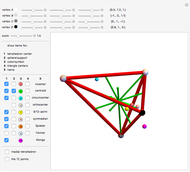
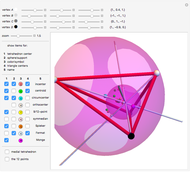
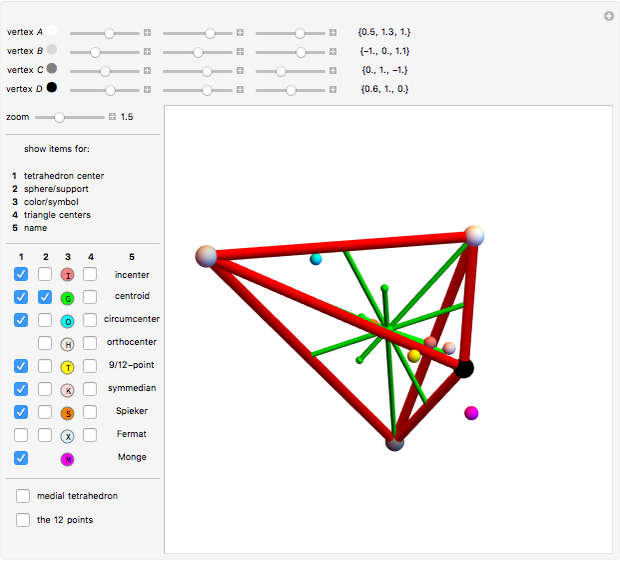
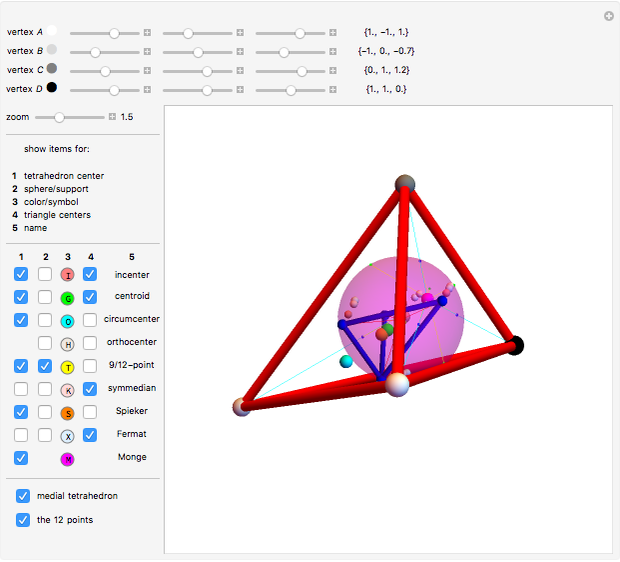
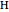There are over 11000 known triangle centers [1], each of which has a corresponding function with the properties of homogeneity, bisymmetry and cyclicity. Some of the centers of a triangle △ have a corresponding point in a tetrahedron T.
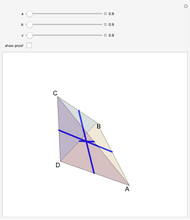
△ Incenter  , where the angle bisectors intersect; the center of the incircle.
, where the angle bisectors intersect; the center of the incircle.
T center of the insphere, which is tangent to the four faces.
△ Centroid  , where the medians intersect.
, where the medians intersect.
T Center of mass, the mean of the four vertices.
△ Circumcenter  , the center of the circumcircle.
, the center of the circumcircle.
T Center of the circumsphere, which goes through the four vertices.
△ Orthocenter  , where the altitudes intersect.
, where the altitudes intersect.
T No corresponding center. When altitudes are concurrent, same as Monge point.
△ 9-point  , the center of the nine-point circle.
, the center of the nine-point circle.
T Center of the 12-point sphere.
△ Symmedian  , reflections of the medians in the angle bisectors.
, reflections of the medians in the angle bisectors.
T Reflections of the median planes in the dihedral angle bisectors. Also the least-squares point, which is the point with minimal total distance to the four faces.
△ Spieker  , incenter of the medial triangle.
, incenter of the medial triangle.
T Insphere of the medial tetrahedron.
△ Monge  , not a triangle center.
, not a triangle center.
T Concurrence of six midplanes, each through an edge midpoint and perpendicular to the opposing edge.
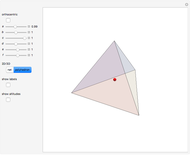
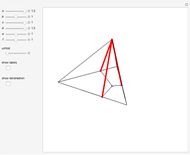
△ Fermat  , the point that minimizes the sum of the distances to the vertices.
, the point that minimizes the sum of the distances to the vertices.
T Minimize sum of distances to vertices. Construct a sphere  with three vertices and the Fermat point. Construct a segment from the fourth vertex through the Fermat point to the other intersection point with
with three vertices and the Fermat point. Construct a segment from the fourth vertex through the Fermat point to the other intersection point with 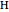 . Repeat to make four Fermat segments, all with length equal to the total distance of the Fermat point to the four vertices.
. Repeat to make four Fermat segments, all with length equal to the total distance of the Fermat point to the four vertices.
Each triangle center has an elegant function for the barycentric or trilinear coordinates of the point. So far, no corresponding elegant set of functions for the tetrahedral centers is known. Ideally, given the four face areas, four face perimeters, four solid angles, four vertex altitudes, four exspheres, six dihedral angles, six edge lengths or 12 face angles, some subset should fit into some function. This notebook can generate thousands of tetrahedral centers. First, generate the four points of a triangle center, then apply one of the tetrahedral methods above. For example, T △
△ would find the tetrahedral symmedian point for the four orthocenters.
would find the tetrahedral symmedian point for the four orthocenters.
[less]