The 12x12 Queens Problem

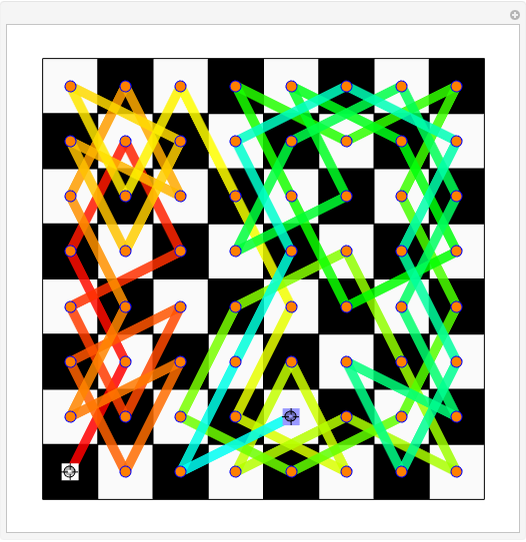
A classic puzzle is to arrange 5 differently colored sets of 5 queens on a 5×5 board so that no two queens of the same color attack each other. For 8 sets of 8 queens on an 8×8 board, the problem has no solution. How about 12 sets of 12? George Pólya showed that a doubly periodic solution for the -queens problem exists if and only if . For years, due to this result, it was assumed that 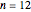was unsolvable. Patrick Hamlyn and Guenter Stertenbrink tackled it anyway, using a clique-search program in the graph of all 14200 12-queen solutions. It turns out there are 178 solutions, displayed here.