Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The 2-(64,8,1) Design

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

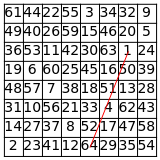
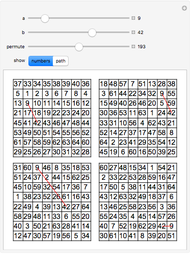
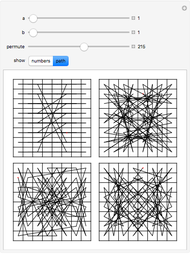
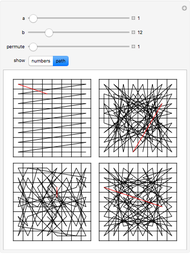
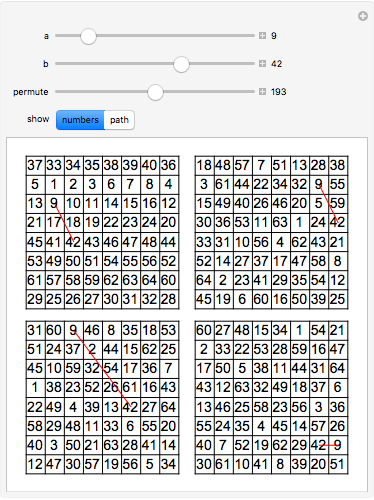
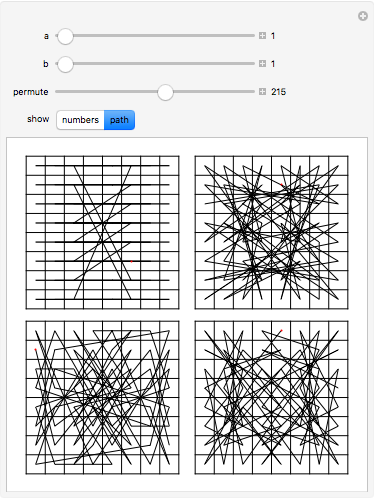
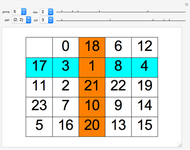
The combinatorial design 2-(64,8,1) can be represented with four squares. For any 2 integers chosen up to 64, there is exactly 1 length-8 row, column, or diagonal that contains the pair. Each square can be modified by one of the 8!! = 384 permutations that preserve rows, columns, and diagonals. Combinatorially, 2-(64,8,1) is unique.

[more]

The 2-(16,4,1) design can be found in the Magic Squares and Designs Demonstration, and is also combinatorially unique. Designs exist for 2-(25,5,1), 2-(49,7,1), 2-(81,9,1), 2-(121,11,1), and 2-(169,13,1), but they would not be squares with diagonals. No designs exist for either 2-(36,6,1) or 2-(100,10,1). Whether 2-(144,12,1) exists is a long-unsolved question.

[less]

Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send