The Appeals Court Paradox

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
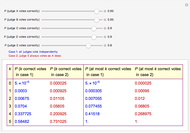
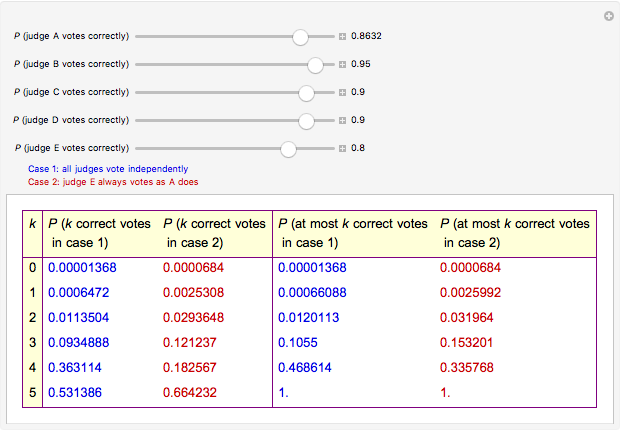
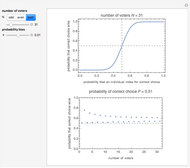
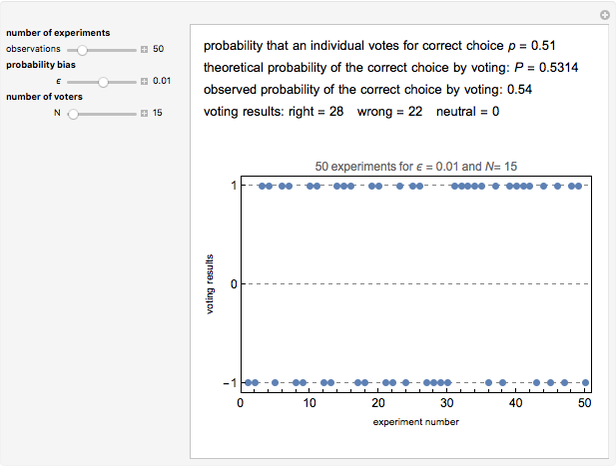
A criminal appeals court consists of five judges: A, B, C, D, and E. Consider two cases: in case 1, each judge votes independently, and in case 2, judge E always votes as judge A does. This Demonstration shows the probabilities of various numbers of correct decisions in each case.
[more]
Contributed by: Heikki Ruskeepää (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: This is the example already explained the caption. In case 1, the court makes an incorrect decision with probability 0.007055 (this is the probability that we get at most two correct decisions), while in case 2, that probability, 0.012, is almost twice as large as in case 1.
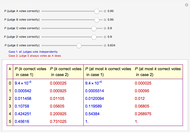
Snapshot 2: To get as high a probability of an incorrect decision in case 1 as in case 2 (that is, 0.012), we have to set the probability that judge E makes a correct decision to as low a value as 0.624.
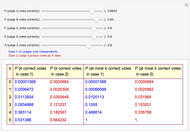
Snapshot 3: Another way to get as high a probability of an incorrect decision in case 1 as in case 2 (that is, 0.012) is to set the probability that judge A makes a correct decision to as low a value as 0.8632.
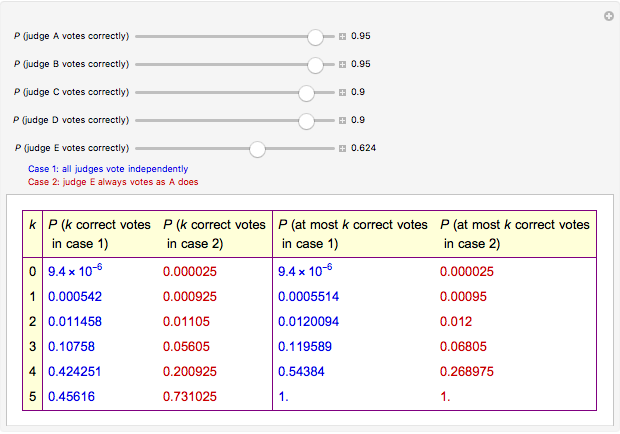
Snapshot 4: The Demonstration can also be used to calculate probabilities of various numbers of successes in other situations of independent experiments. As an example, consider three hunters. When they independently shoot at the same hare, their probabilities of a hit are 0.01, 0.05, and 0.08. Snapshot 4 shows that the probabilities of 0, 1, 2, and 3 hits are 0.86526, 0.12952, 0.00518, and 0.00004, respectively. (In this example, case 2 is not relevant.)
As an example of how the probabilities are calculated, first consider case 1 and only three judges: A, B, and C. If the probabilities that the judges make a correct decision are  ,
,  , and
, and  , respectively, the probabilities of 0, 1, 2, and 3 correct decisions are:
, respectively, the probabilities of 0, 1, 2, and 3 correct decisions are:
 ,
,
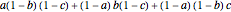 ,
,
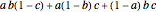 ,
,
and 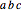 ,
,
respectively. You can get these results with the command pr1[{a, b, c}, k], k = 0, 1, 2, 3 (the function pr1 is defined in the initialization section of the Demonstration). The probabilities are calculated similarly if we have five judges (you can get these probabilities with pr1[{a, b, c, d, e}, k], k = 0, ..., 5).
In case 2, the probabilities of 0, 1, 2, 3, 4, or 5 correct decisions are defined in the function pr2 in the initialization section of the Demonstration; now you can practically ignore judge E and always double the vote of judge A. For example, to get three correct decisions, EITHER judge A makes the correct decision and one of B, C, and D also makes the correct decision OR A makes the wrong decision and B, C, and D all make the correct decision; the probability of three correct decisions is thus 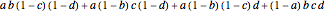 .
.
This Demonstration is based on problem 16 in [1], which is in turn based on an example in [2, p. 171].
References
[1] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton, NJ: Princeton University Press, 2008.
[2] G. J. Székely, Paradoxes in Probability Theory and Mathematical Statistics, Dordrecht: D. Reidel, 1986.
Permanent Citation