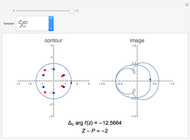
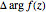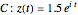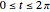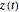The Argument Principle in Complex Analysis

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
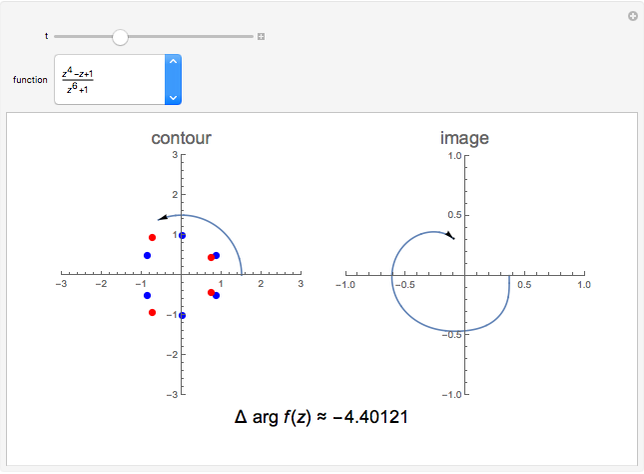
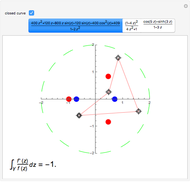
Let 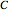 be a closed contour parameterized by
be a closed contour parameterized by  in the range
in the range 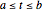 , and
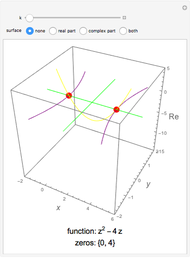
, and 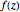 a function meromorphic inside and on
a function meromorphic inside and on 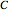 . Define
. Define 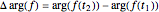 for some
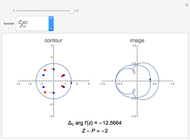
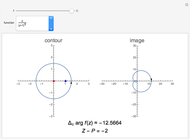
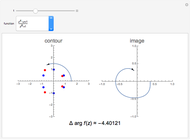
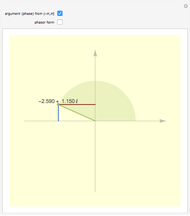
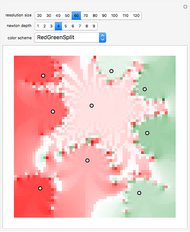
for some  . The argument principle relates the change in argument of
. The argument principle relates the change in argument of 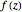 as
as  describes
describes 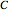 once in the positive direction to the number of zeros and poles inside the contour. The change in argument for one complete circuit around
once in the positive direction to the number of zeros and poles inside the contour. The change in argument for one complete circuit around 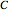 is given by
is given by  . The Argument Principle then states:
. The Argument Principle then states:  , where
, where  and
and  are the number of zeros and poles inside the contour, counting multiplicities.
are the number of zeros and poles inside the contour, counting multiplicities.
Contributed by: Dominic Milioto (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation