The Begonia Point
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
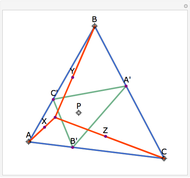
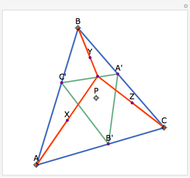
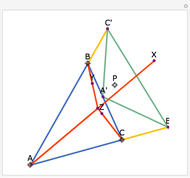
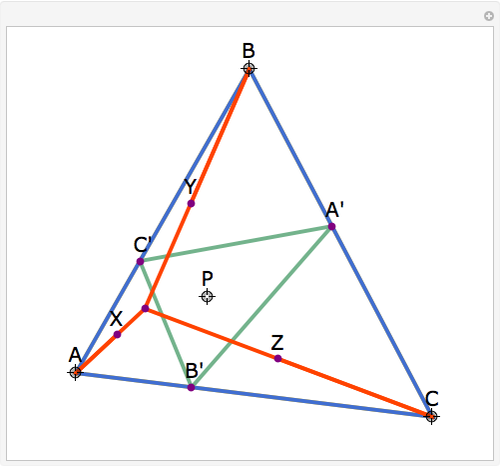
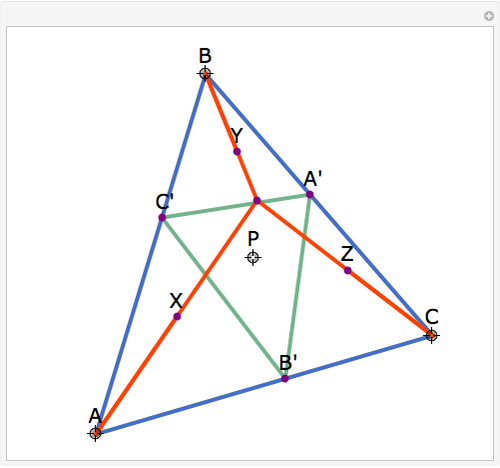
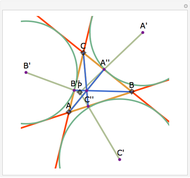
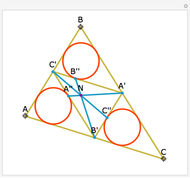
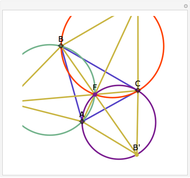
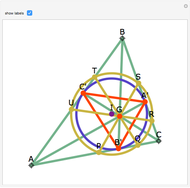
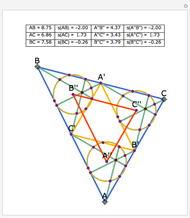
Let ABC be a triangle and let P be a point. Let A'B'C' be the Cevian triangle of P, which means that A', B', and C' are the intersections of AP, BP, and CP with BC, CA, and AB, respectively. Let X, Y, and Z be the reflections of P in B'C', C'A', and A'B', respectively. Then AX, BY, and CZ are concurrent. The name "begonia point" has been suggested for this point of concurrency.
Contributed by: Jay Warendorff (October 2008)
After work by: Darij Grinberg
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation