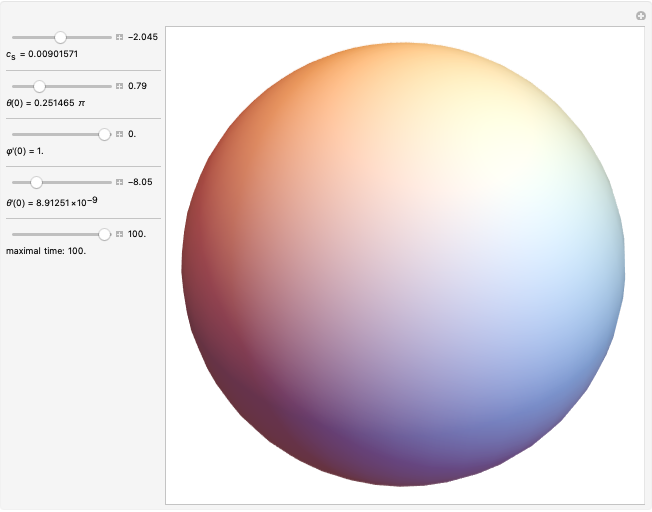
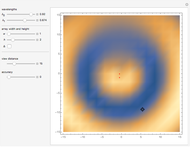
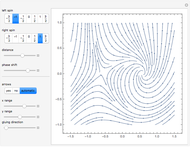
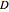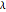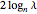The Boundary of Periodic Iterated Function Systems
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
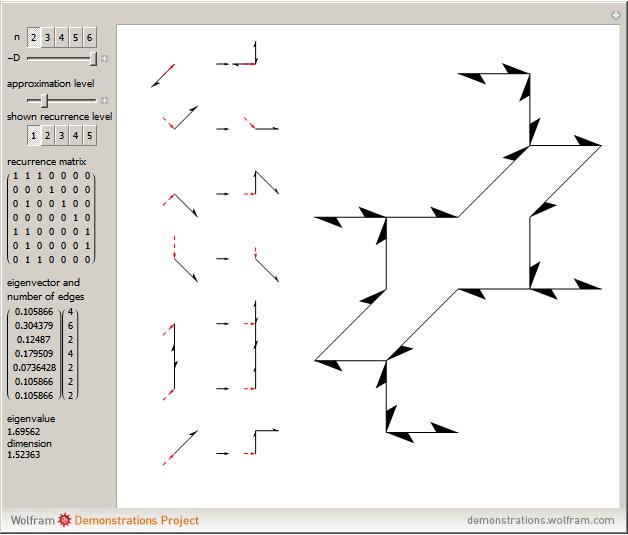
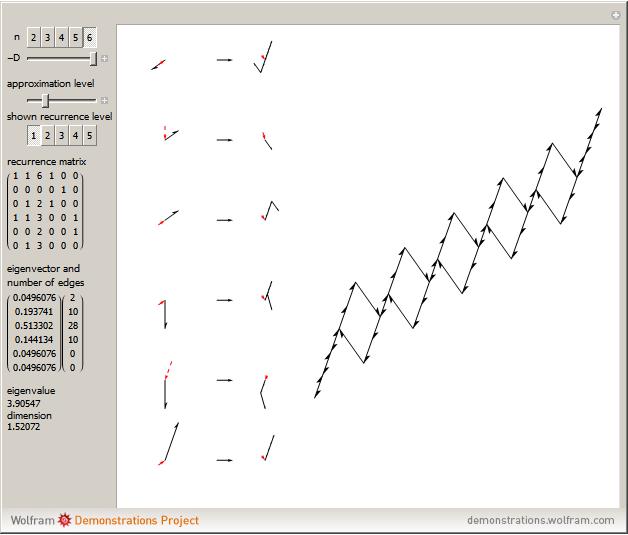
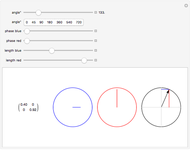
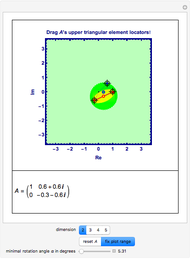
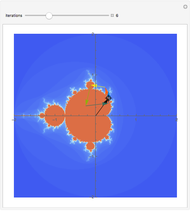
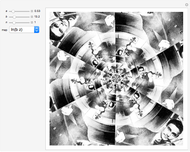
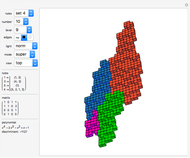
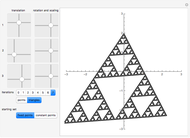
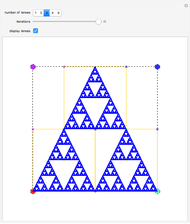
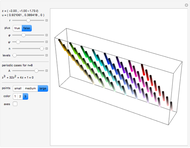
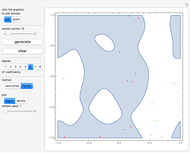
This Demonstration shows approximations of the boundary (clockwise) of some discrete families of iterated functional systems (IFS), 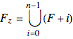 , which can be thought of as the fractional part of numeration systems with a complex base,
, which can be thought of as the fractional part of numeration systems with a complex base, 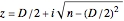 .
.
Contributed by: Jarek Duda (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For information on the theory behind this Demonstration, see: http://xxx.arxiv.org/pdf/0712.1309
Permanent Citation