The Buffon Noodle Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
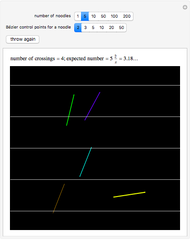
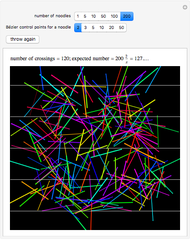
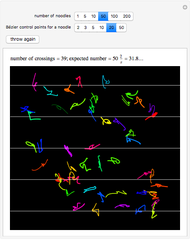
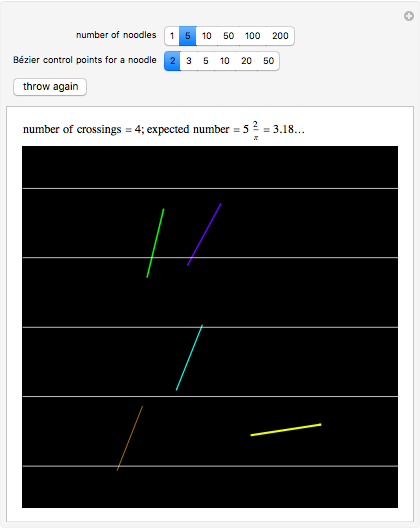
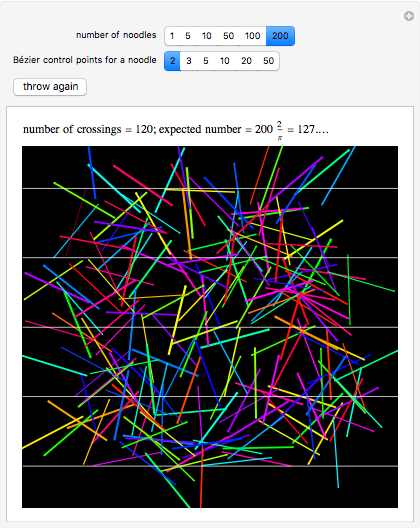
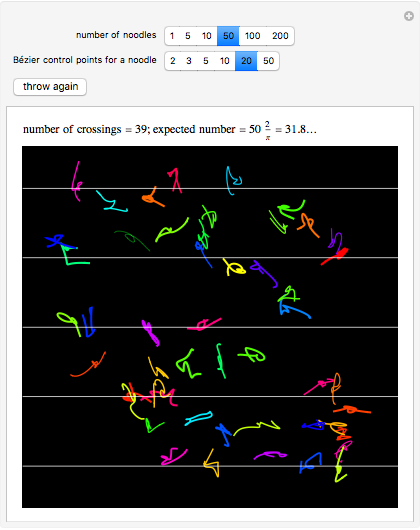
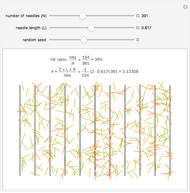
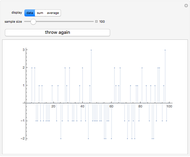
The Buffon noodle problem is an extension of the Buffon needle problem: curves of unit length are dropped randomly onto a plane marked with lines one unit apart. If crossing multiplicities are taken into account (i.e., a noodle crossing a line  times contributes
times contributes  to the total crossing count), then the expected number of crossings is
to the total crossing count), then the expected number of crossings is  , where
, where  is the number of noodles thrown. This is the same result as the classic needle problem, where the probability of a crossing is
is the number of noodles thrown. This is the same result as the classic needle problem, where the probability of a crossing is  .
.
Contributed by: Stan Wagon (Macalester College) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
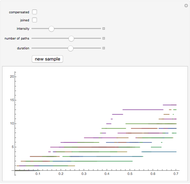
Each noodle is created by using a Bézier curve constructed from random points and then truncating the curve so that its arc length is exactly 1. The proof of the result on the expected number of crossings is not difficult and can be found in the following paper.
J. F. Ramaley, "Buffon's Noodle Problem," American Mathematical Monthly, 76(8), 1969 pp. 916–918.
Permanent Citation
"The Buffon Noodle Problem"
http://demonstrations.wolfram.com/TheBuffonNoodleProblem/
Wolfram Demonstrations Project
Published: March 7 2011