The Coase Theorem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
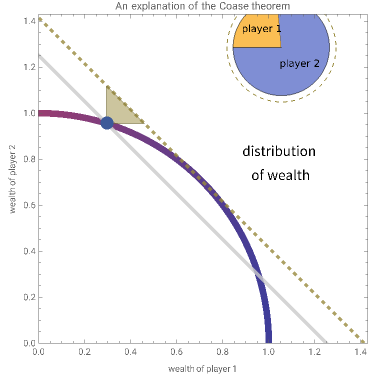
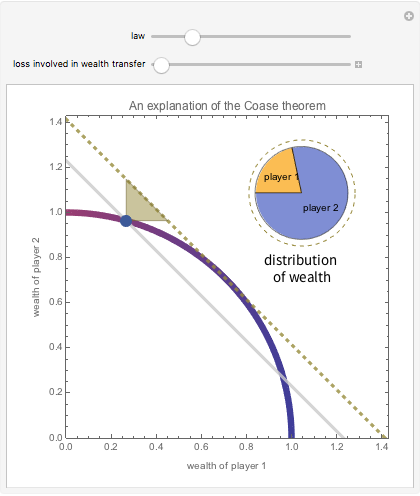
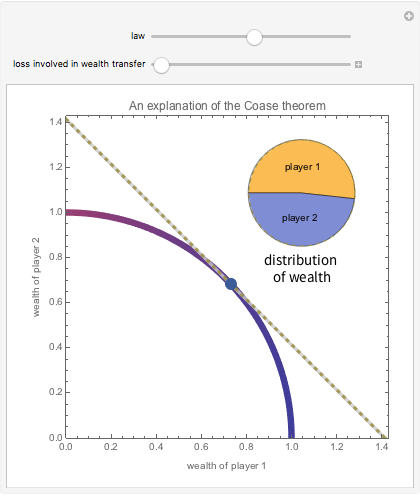
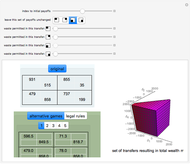
The Coase theorem is a centerpiece in the economic analysis of law. It asserts that, so long as bargaining is costless and contracts can be costlessly enforced, the default rule of law will not affect economic efficiency. This is so because if the default rule (the one that applies in the absence of agreement to the contrary) is not "efficient", the amount of gain attainable by negotiating a more efficient law will permit both parties to be better off as a result of the change. Indeed, the parties will bargain for the most efficient law. If, however, there are costs associated with bargaining (the cost of meetings, contracting, enforcement) or there is a risk of impasse, the initial selection of law will affect the efficiency of the outcome. This Demonstration illustrates the Coase theorem by letting you select (a) the default rule and (b) the costs associated with bargaining. The Demonstration outputs (a) a graphic using a blue point to depict the distribution of wealth resulting from that default rule; (b) a gray line showing all distributions of wealth whose total is the same as that produced by the default rule; (c) a green dashed line showing all distributions of wealth whose total is the same as that produced by the most efficient rule; and (d) a locus tracing the trajectory of wealth distributions over the set of possible laws, color coded to reflect the wealth of player 1. It also displays green triangles showing the set of wealth distributions that would (a) leave no player worse off than at the default rule and (b) are feasible given appropriate changes in the rule of law. Inset at the top right is a pie chart showing the total wealth produced by the current default rule and the resulting distribution of wealth. A green dashed circle shows the size of the pie that would be generated if the default rule were also the efficient rule. Various tooltips provided in the graphic help explain matters further.
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
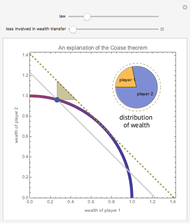
Snapshot 1: Although the default rule is favorable to player 2, player 1 can improve his position by paying player 2 to shift to the efficient rule. Player 2 can be made better off as a result of this bargain.
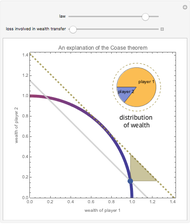
Snapshot 2: Although the default rule is favorable to player 1, player 2 can improve his position by paying player 1 to shift to the efficient rule. Player 1 can be made better off as a result of this bargain.
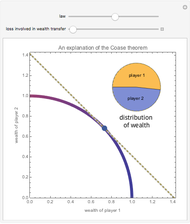
Snapshot 3: The default rule is efficient. There is no need for costly bargaining.
The green triangle illustrates the way in which the choice of default rule constrains the final distribution of wealth.
The author of the Coase theorem, Ronald Coase, won a Nobel Prize in economics for this and other work. His article announcing the theorem is one of the most cited in all of economics. Discussion and criticism of the theorem is summarized in the online version of the Encyclopedia of Law and Economics.
R. H. Coase, "The Problem of Social Cost," Journal of Law and Economics, 3, Oct 1960 pp. 1-44.
Permanent Citation
"The Coase Theorem"
http://demonstrations.wolfram.com/TheCoaseTheorem/
Wolfram Demonstrations Project
Published: March 7 2011