The Complex Exponential
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
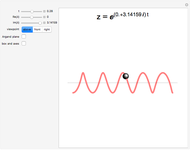
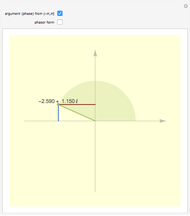
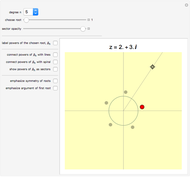
This Demonstration plots the complex exponential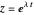 
. In the starting orientation ("above"), 
increases from -5 on the left to 5 on the right. You are looking down on the Argand plane along the positive imaginary axis—turn on the "Argand plane" checkbox to see it. (Note: animations may be jerky with this option on.) The real and imaginary parts of 
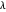are controlled by the real and imaginary sliders. In the starting position, 
, and the plot is a left-handed helix. The 
slider controls the position of the gray ball.
Contributed by: Leon Avery (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
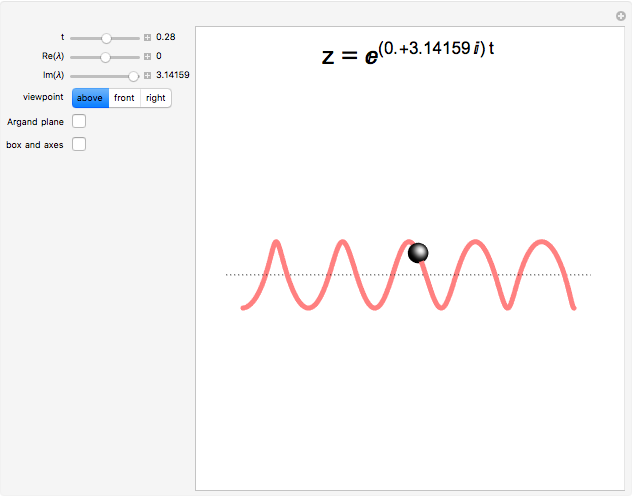
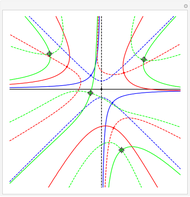
Once you are familiar with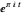 
, play with the imaginary slider to see how it controls the frequency and handedness of the helix. Now return to the "above" viewpoint, set the imaginary slider as close as you can to 0, then play with the real slider. You see the familiar real exponential.
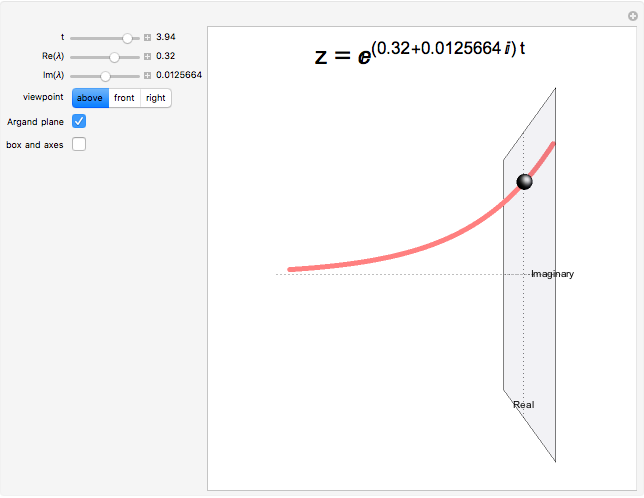
Set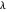 
to about 
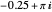and play with the 
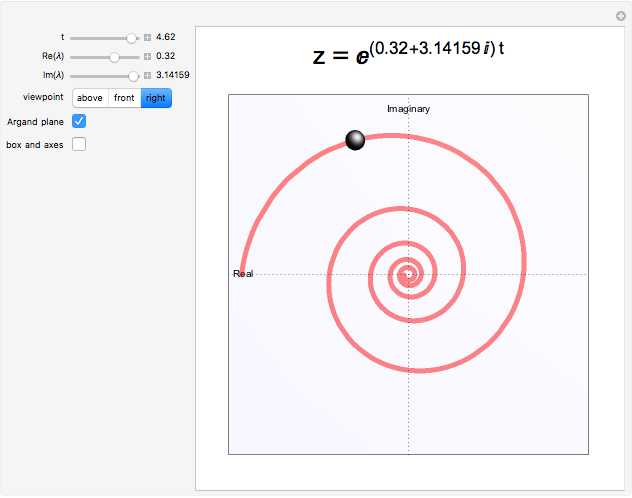
slider. This is a shrinking spiral. A dynamic system with this time evolution is spiraling in toward a stable fixed point. Set 
to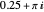 
. This is an expanding spiral, such as you might see in the vicinity of an unstable fixed point. Look at this from the right viewpoint.
Permanent Citation
Complex Number
?tefan Porubský
Complex Polynomials
Ed Pegg Jr
Complex Slide Rule
Michael Rogers (Oxford College of Emory University)
Complex Newton Map
Ed Pegg Jr
Complex Power Plot
Sue Hurley
Powers of Complex Roots
Eliot Ball
Complex Numbers with Different Norms
Izidor Hafner
Powers of Complex Points
Ed Pegg Jr
Maps of a Complex Variable
Douglas N. Arnold
Roots of Complex Numbers
John Kiehl
