Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

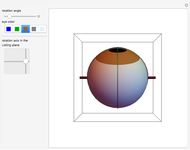
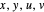The Complex Unit Circle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

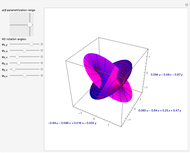
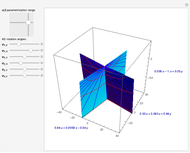
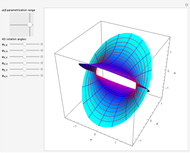
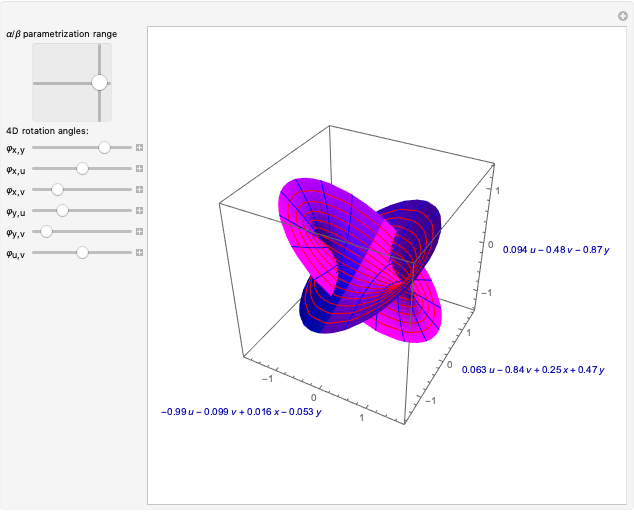
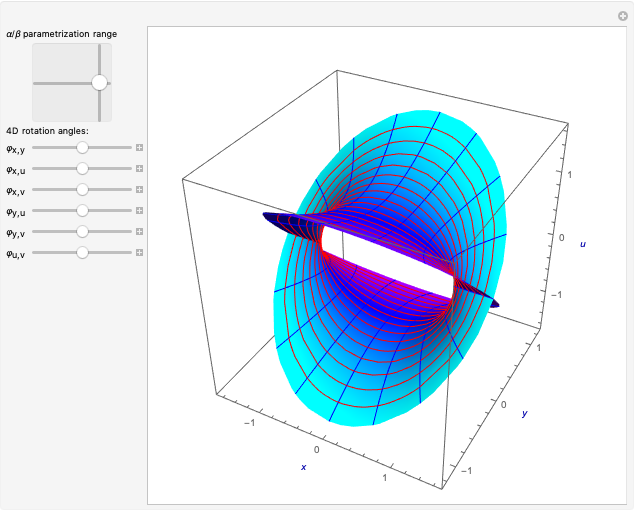
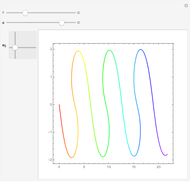
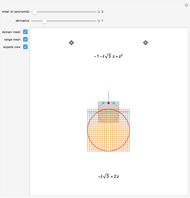
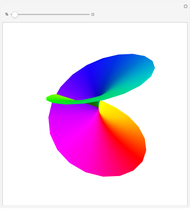
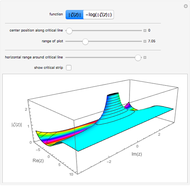
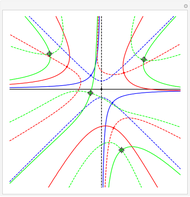
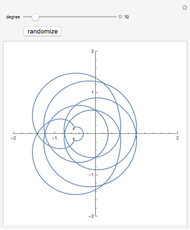
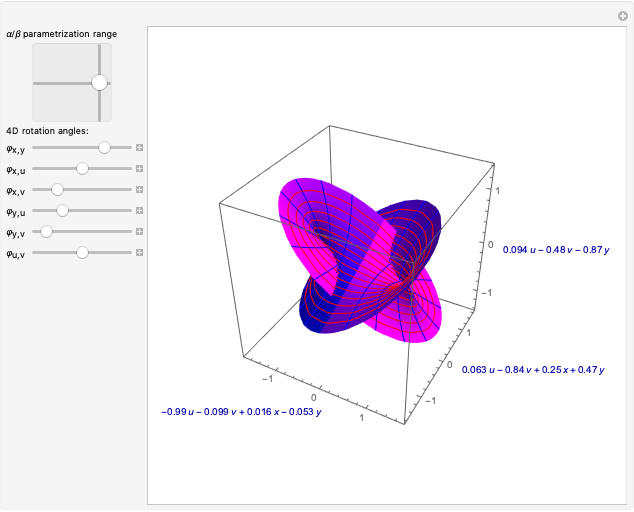
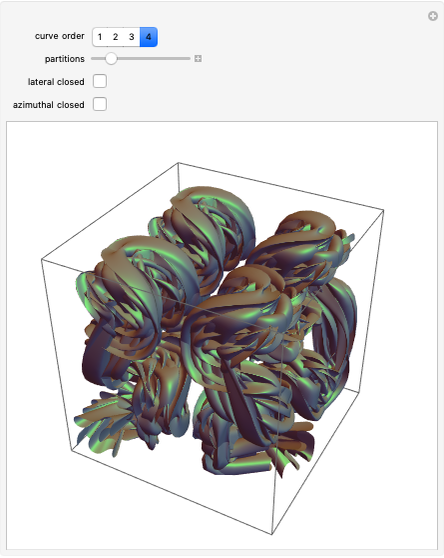
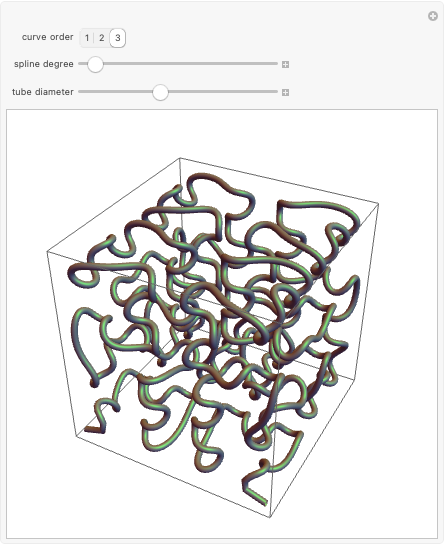
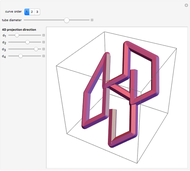
The points of the complex unit circle can be parametrized:

[more]

,

.

This Demonstration shows 3D projections of the surface in space. The angles denote the rotation angles inside the hyperplane. In the limit, as , the complex unit circle becomes a circle in the plane.

[less]

Contributed by: Michael Trott with permission of Springer (March 2011)
From: The Mathematica GuideBook for Graphics, second edition by Michael Trott (© Springer, 2008).
Open content licensed under CC BY-NC-SA

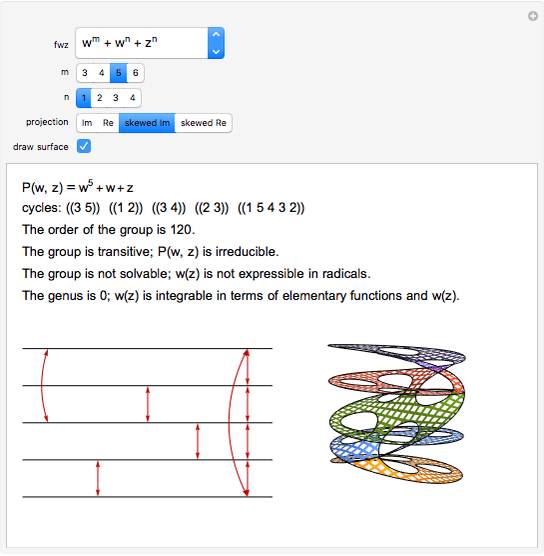
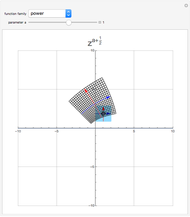
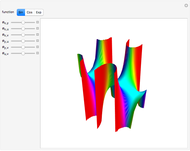
Snapshots

Details

For a detailed discussion of the complex unit circle, see

R. Hammack, "A Geometric View of Complex Trigonometric Functions," College Mathematics Journal, 38(3), 2007 pp. 210-217.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send