Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

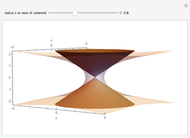
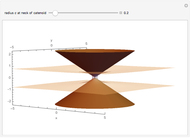
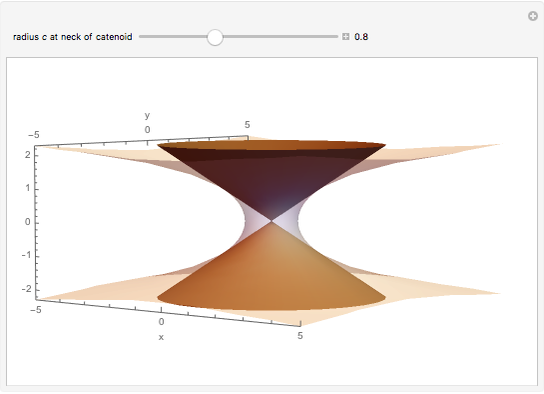
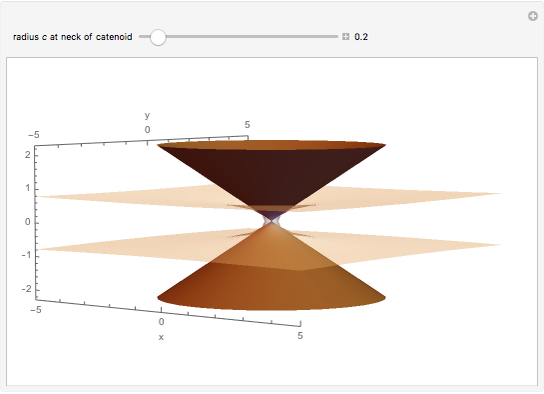
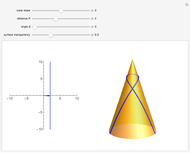
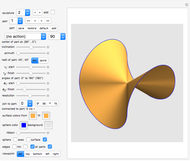
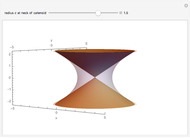
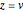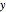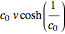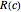The Cone Limit of the Catenoid

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Consider the catenoids given by the parametric equations

[more]

,

,

,

where is a positive parameter that you can vary.

When , this reduces to the equation of a circle in the - plane of radius centered at the origin.

For a given height , let . The slope of the cone is , where is the value that minimizes . This cone is unique; its horizontal slices are circles with radii that are the greatest lower bound of the radii of the horizontal slices of the catenoids at the same height; the catenoid intersects the interior of any larger cone.

[less]

Contributed by: Jennifer Zering (December 2013)
With additional contributions by: Nelson Castañeda, Central Connecticut State University
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] E. Abbena, S. Salamon, and A. Gray, Modern Differential Geometry of Curves and Surfaces with Mathematica, 3rd ed., Boca Raton: Chapman and Hall/CRC, 2006.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send