Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Conjugate Locus on the Triaxial Ellipsoid

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

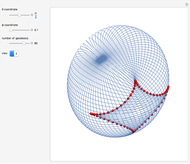
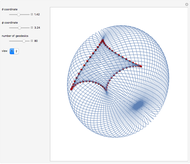
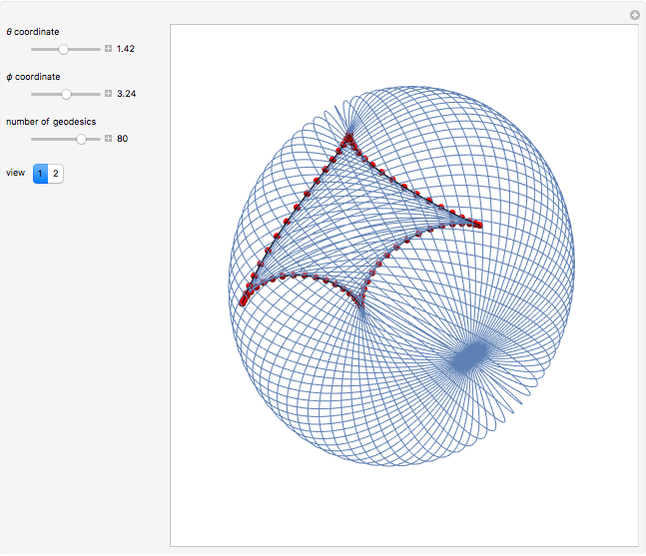
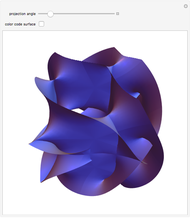
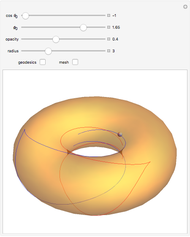
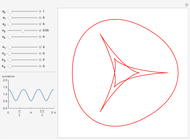
The "last geometric statement of Jacobi" says, among other things, that the conjugate locus of a non-umbilic point on the triaxial ellipsoid has four cusps. This was only recently proved by Itoh and Kiyohara [1].

[more]

In this Demonstration we show the locus of conjugate points along a "spray" of unit speed geodesics emanating from a "base point" on the ellipsoid with semiaxes 1, 1.2, and 1.5. You can vary the coordinates of the base point and the number of geodesics in the spray. We also offer two different views (in the second view, the blue sphere is the base point).

[less]

Contributed by: Thomas Waters (April 2014)
Open content licensed under CC BY-NC-SA

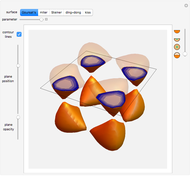
Snapshots

Details

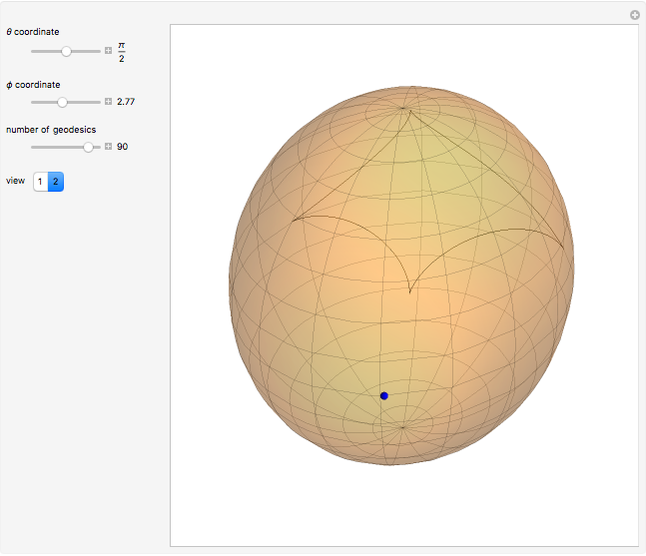
The parameterization of the ellipsoid used is 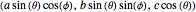, with , , 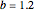and .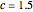

It can be a little slow to render the image after dragging the and controls. Having said that, Mathematica is solving, for each and , the geodesics equations and the Jacobi equation tens of times, so it is still impressive what Mathematica can do.

Try to find the umbilic points; these are base points where the conjugate locus degenerates to a point (the antipode).

Reference

[1] J. Itoh and K. Kiyohara, "The Cut Loci and the Conjugate Loci on Ellipsoids," Manuscripta Mathematica, 114, 2004 pp. 247–264.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send