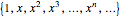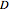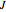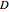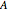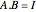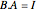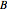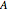The Derivative and the Integral as Infinite Matrices
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
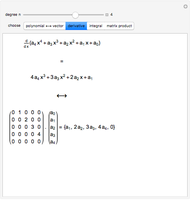
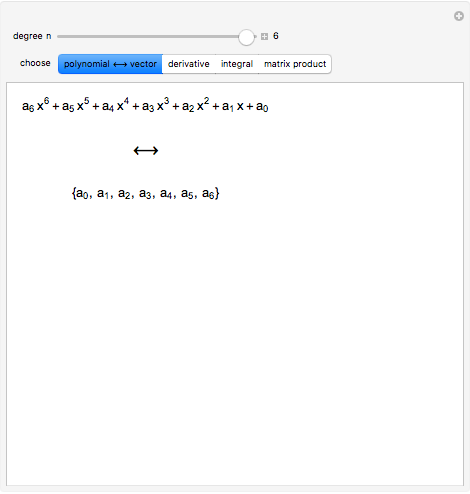
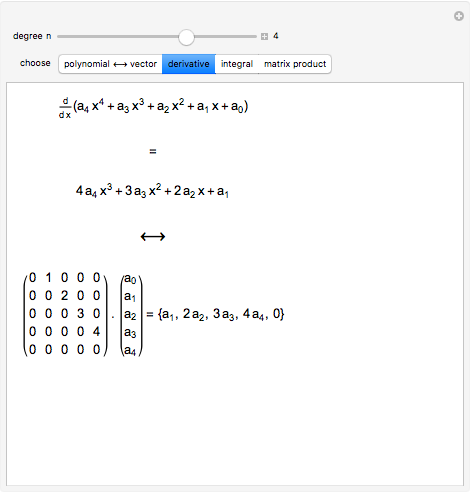
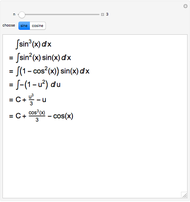
A polynomial 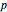 can be encoded as a vector
can be encoded as a vector  using the coefficients of
using the coefficients of 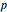 as the entries of
as the entries of  . In this Demonstration column vectors are shown using round parentheses (like these) and row vectors using braces {like these}.
. In this Demonstration column vectors are shown using round parentheses (like these) and row vectors using braces {like these}.
Contributed by: George Beck (March 2017)
Open content licensed under CC BY-NC-SA
Details
Snapshots
Permanent Citation