The Dual Basis for the Tangent Space of a 2D Surface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
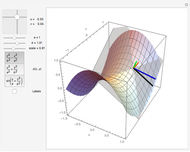
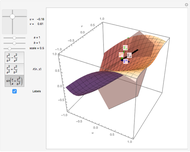
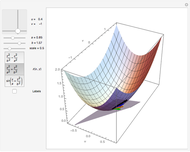
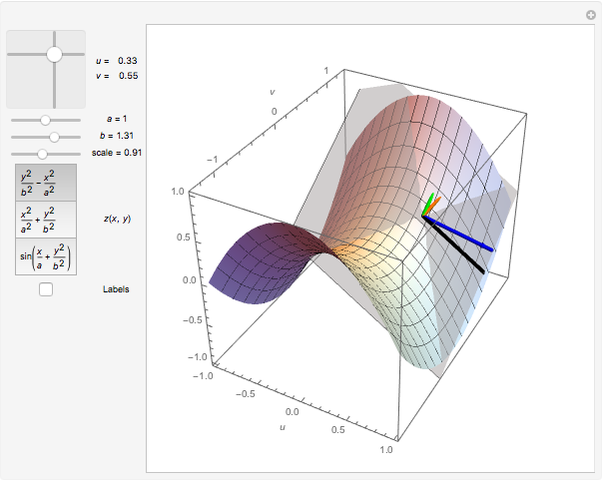
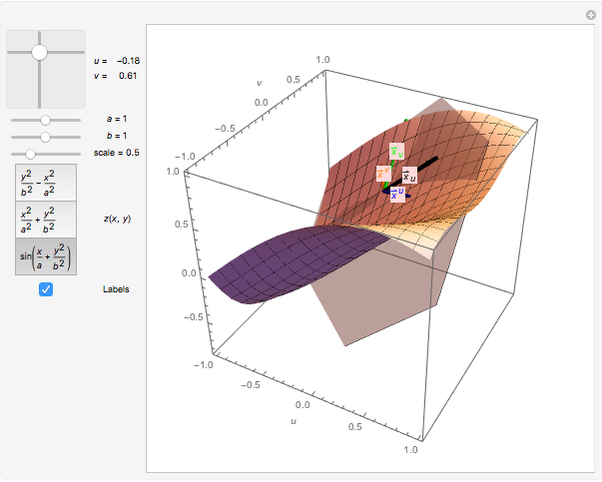
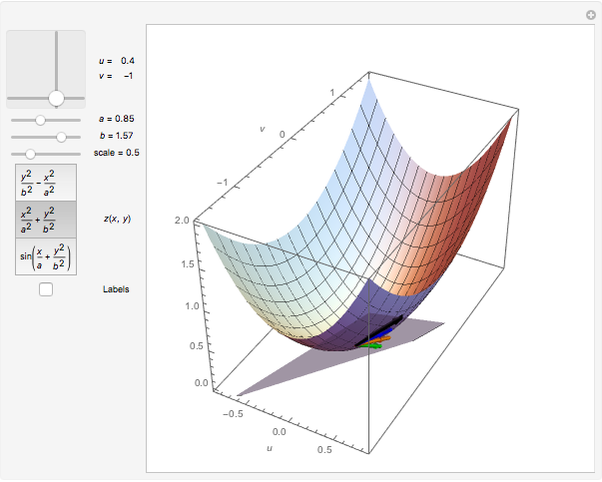
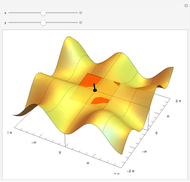
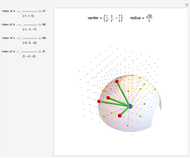
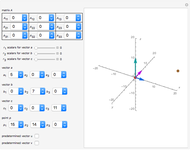
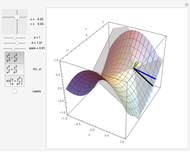
This Demonstration illustrates the tangent plane basis and the reciprocal basis at points along a few sample surfaces. The tangent plane itself is shown and a control is provided to alter the position of the tangent plane along the surface. This lets you see the normality of the tangent plane basis vectors and their alternate indexed reciprocal vector. You can also compare the orientations of the tangent plane basis vectors with their reciprocals, and see how these pairs of vectors are not necessarily collinear.
Contributed by: Peeter Joot (March 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A 3D surface can be represented in a parameterized vector form using two parameters  and
and  as
as 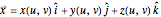 . The partial derivatives
. The partial derivatives 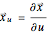 and
and 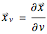 with respect to these parameters provide a basis
with respect to these parameters provide a basis 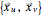 for the tangent plane at the point of evaluation. Because those vectors are not necessarily orthogonal, the reciprocal (or dual) vectors
for the tangent plane at the point of evaluation. Because those vectors are not necessarily orthogonal, the reciprocal (or dual) vectors 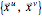 for the tangent plane can be useful for expressing projection operations. These vectors satisfy the relationship
for the tangent plane can be useful for expressing projection operations. These vectors satisfy the relationship 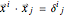 , for
, for 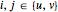 .
.
This Demonstration shows both the tangent plane basis 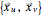 and the reciprocal basis
and the reciprocal basis 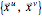 for a few sample surfaces, and controls for altering those surfaces. You can use the scale control to adjust the length of both pairs of bases should they range out of the image or be too small for visibility. A control for adjusting the
for a few sample surfaces, and controls for altering those surfaces. You can use the scale control to adjust the length of both pairs of bases should they range out of the image or be too small for visibility. A control for adjusting the 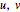 parameters is also provided.
parameters is also provided.
The reciprocal vectors for a two-dimensional subspace basis 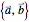 can be calculated using the following geometric algebra expression:
can be calculated using the following geometric algebra expression:
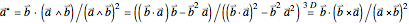
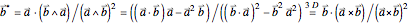 ,
,
or, in 3D using dual cross product representation (also above). Note that the geometric algebra square of a vector equals the squared norm of that vector.
Additional background material on the calculation and applications of the reciprocal basis to nonorthonormal coordinate systems can be found in [1].
Reference
[1] A. Macdonald, Vector and Geometric Calculus, CreateSpace Independent Publishing Platform, 2012.
Permanent Citation