The Esscher Transform of the Densities of a Symmetric NIG Lévy Process

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
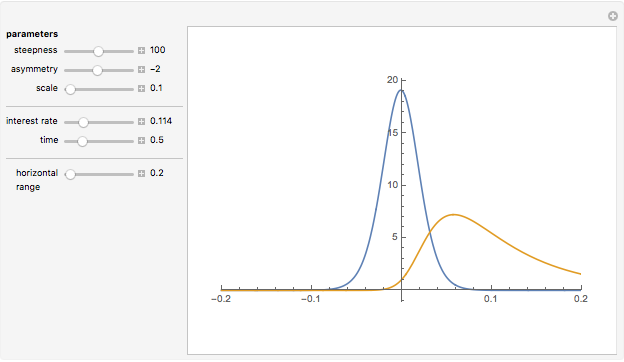
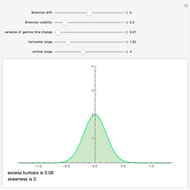
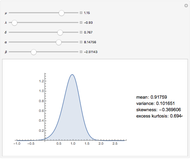
This Demonstration illustrates the effect of applying the Esscher transform to one-dimensional densities when the logarithm of the price process is the so-called Normal Inverse Gaussian (NIG) Lévy process. The distribution of this process is determined by four parameters  ,
, 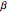 ,
,  , and
, and  : steepness, asymmetry, scale, and location. The location parameter is set to 0 (in other words, the process is centered), which makes the implementation of the Esscher transfer particularly simple (while at the same time being quite acceptable, on empirical grounds, for modeling stock prices). We display on the same graph the density of the logarithm of the price process at a given time
: steepness, asymmetry, scale, and location. The location parameter is set to 0 (in other words, the process is centered), which makes the implementation of the Esscher transfer particularly simple (while at the same time being quite acceptable, on empirical grounds, for modeling stock prices). We display on the same graph the density of the logarithm of the price process at a given time  , and the density of the process obtained by applying to it the Esscher transform. It is the latter density that is used in computing option prices.
, and the density of the process obtained by applying to it the Esscher transform. It is the latter density that is used in computing option prices.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The fundamental theorem of asset pricing (e.g., [1]) states (loosely speaking) that the arbitrage-free prices of "contingent claims" (e.g., options) on an asset (e.g., a stock) whose price follows a (semi-martingale) stochastic process can be computed as expected values of the discounted payoff, but not (as was once thought) under the "real world measure", but under a measure equivalent to it and having the property that the discounted price process of the asset is a local martingale with respect to it. In the case of the classical Black–Scholes model, this "equivalent martingale measure" is unique and is obtained by changing the "drift" of the logarithm of the price process (the Girsanov theorem). However, in more realistic models, such as those involving jumps or stochastic volatility, there are usually infinitely many equivalent martingale measures and one has to choose one based on economic considerations. One such measure that is frequently used is obtained by means of the so-called Esscher transform, which had a long history of being used in actuarial mathematics before being introduced to option pricing by Gerber and Shiu [2]. For a Lévy process, the Esscher transform can be defined by transforming the one-dimensional marginal densities in the manner of [1]. The transformed marginal densities  depend on a single parameter
depend on a single parameter  and are related to the original marginal densities
and are related to the original marginal densities  by the relation
by the relation 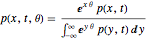 . By writing down the condition that the transformed process is a martingale, you can obtain an equation for the parameter
. By writing down the condition that the transformed process is a martingale, you can obtain an equation for the parameter  . In the case of the centered (i.e., when the location parameter
. In the case of the centered (i.e., when the location parameter  ) NIG process, considered in this Demonstration, the equation takes a particularly simple form (see [3], p. 28) and the marginal densities of the transformed process are also centered NIG densities. We note that, as shown on page 4 of [4], for certain parameter values an exponential NIG process may not have an Esscher transform. In such a case only the graph of the real-world marginal PDF will be displayed.
) NIG process, considered in this Demonstration, the equation takes a particularly simple form (see [3], p. 28) and the marginal densities of the transformed process are also centered NIG densities. We note that, as shown on page 4 of [4], for certain parameter values an exponential NIG process may not have an Esscher transform. In such a case only the graph of the real-world marginal PDF will be displayed.
[1] F. Delbaen and W. Schachermayer, The Mathematics of Arbitrage, Berlin-Heidelberg-New York: Springer, 2006.
[2] H. U. Gerber and E. S. W. Shiu, "Option Pricing by Esscher Transforms," Transactions of the Society of Actuaries, 46, 1994 pp. 99–191.
[3] K. Prause, "The Generalized Hyperbolic Model: Estimation, Financial Derivatives, and Risk Measures," PhD thesis, University of Freiburg, 1999.
[4] S. Raible, "Lévy Processes in Finance: Theory, Numerics, and Empirical Facts," PhD thesis, University of Freiburg, 2000.
Permanent Citation