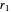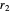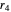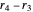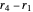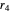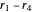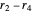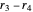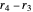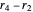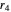Suppose four runners (represented by labeled spheres) run around a circular track. Their speeds are constant integers, 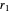 ,
, 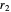 ,
, 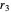 ,
, 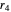 ; assume that
; assume that 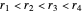 .
.
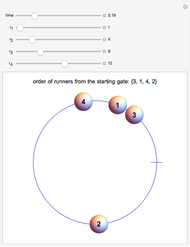
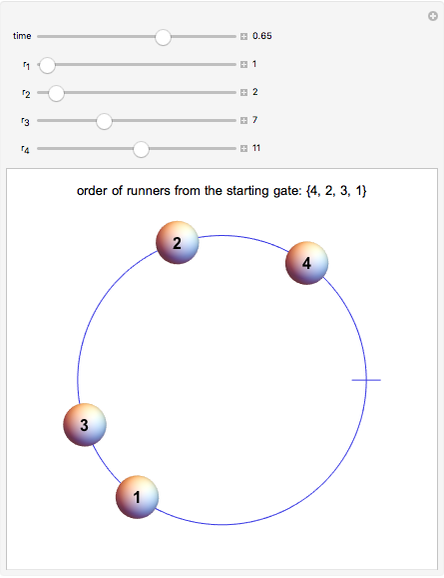
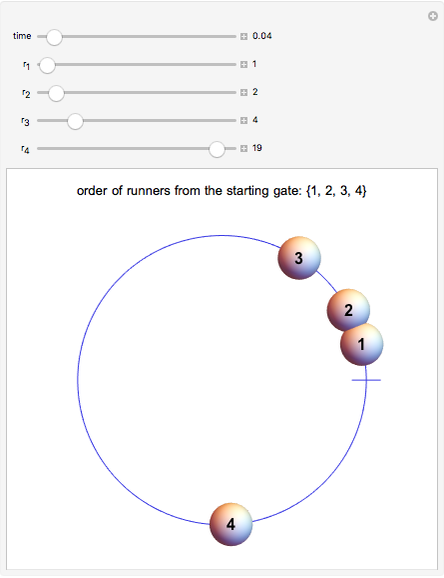
At time 0, all the runners are together at the starting gate; shortly after, they are arranged in the order {1, 2, 3, 4}, counting from the starting gate. The order changes to {4, 1, 2, 3} when runner 4 passes the starting gate. Then either runner 3 passes the starting gate, runner 4 laps runner 1, or the two events happen at the same time, giving possible orders {3, 4, 1, 2}, {1, 4, 2, 3}, or {3, 1, 2, 4}.
In the second half of the race the order mirrors the first half of the race, but in reverse; for instance, just before the end, the order is {4, 3, 2, 1}.
The answer to this question is unknown: which rates generate all 24 possible orders?
For three runners, all six orders are achieved if and only if the two slower rates do not add up to the fast rate.
For four runners, there is a symmetry: the number of permutations achieved for rates 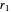 ,
, 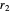 ,
,  ,
, 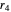 is the same as that for
is the same as that for 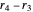 ,
,  ,
, 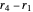 ,
, 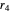 . Here is why. Think of the starting point as runner 0 with rate 0. (Runner 0 breaks the cycle, giving the starting point.) Rotate the plane by
. Here is why. Think of the starting point as runner 0 with rate 0. (Runner 0 breaks the cycle, giving the starting point.) Rotate the plane by  , so that the rates for the five runners are are now
, so that the rates for the five runners are are now  ,
, 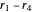 ,
, 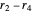 ,
, 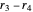 ,
,  . (Runner 4 now becomes stationary.) Look at the plane from the other side: the rates are 0,
. (Runner 4 now becomes stationary.) Look at the plane from the other side: the rates are 0, 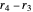 ,
, 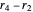 ,
,  ,
, 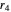 .
.
[less]

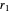 ,
, 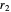 ,
, 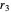 ,
, 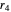 ; assume that
; assume that 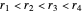 .
.