The Intermediate Axis Theorem Applied to a Ping-Pong Paddle Flip-Over

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
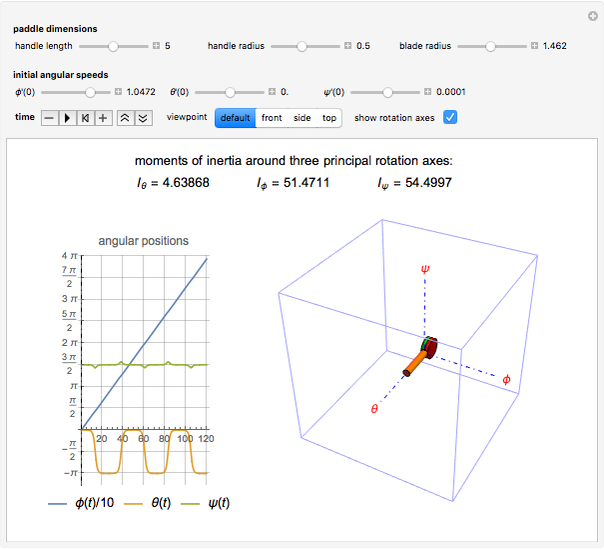
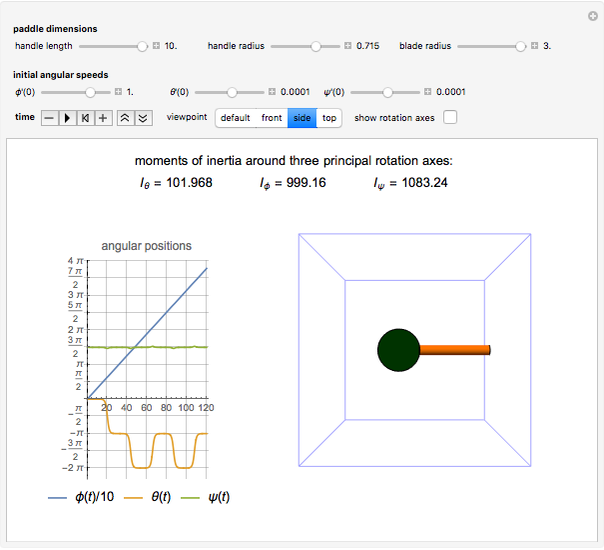
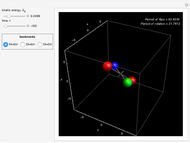
This Demonstration illustrates a theorem in classical dynamics known as the intermediate axis theorem [1].
[more]
Contributed by: Erik Mahieu (June 2015)
Based on work by Mariusz Iwaniuk found at Dzhanibekov Effect or tennis racket theorem
Open content licensed under CC BY-NC-SA
Snapshots
Details
Gravity is neglected in this Demonstration in order to isolate the rotations and avoid translation of the center of mass. This way, the paddle is kept within view of the Graphics3D plot range. This phenomenon was demonstrated in space by the Russian astronaut Vladimir Dzhanibekov [3].
The equations of motion are derived as follows:
There are two conventions for Euler angles; see the Demonstration Euler Angles.
To convert the angular velocities 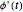 ,
, 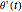 , and
, and  to a fixed coordinate frame, one can use the Euler angles conversion:
to a fixed coordinate frame, one can use the Euler angles conversion:
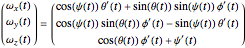 ,
,
which when differentiated gives:
 ,
,
and these can be substituted in the Euler equations of motion (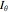 ,
, 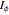 , and
, and 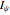 are the moments of inertia around the principal axes):
are the moments of inertia around the principal axes): 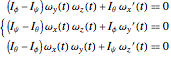
References
[1] D. Schmid, "Stable and Unstable Rotations: The Tennis Racket Theorem," Ask the Van (blog). (Jun 4, 2015) van.physics.illinois.edu/qa/listing.php?id=24571.
[2] E. Johnson. Torque Free Motion of a Rigid Body about Intermediate Inertia Axis [Video]. (Jun 4, 2015)www.youtube.com/watch?v=qEWwIV9Z-eA.
[3] Dzhanibekov Effect in Space (in Russian) [Video]. (Jun 4, 2015) www.youtube.com/watch?v=L2o9eBl_Gzw.
[4] M. Iwaniuk. "Dzhanibekov Effect or Tennis Racket Theorem" from Wolfram Community—A Wolfram Web Resource. (Jun 4, 2015), community.wolfram.com/groups/-/m/t/498246?p_p_auth=PV4kRYzg.
Permanent Citation