The Joukowski Mapping: Airfoils from Circles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
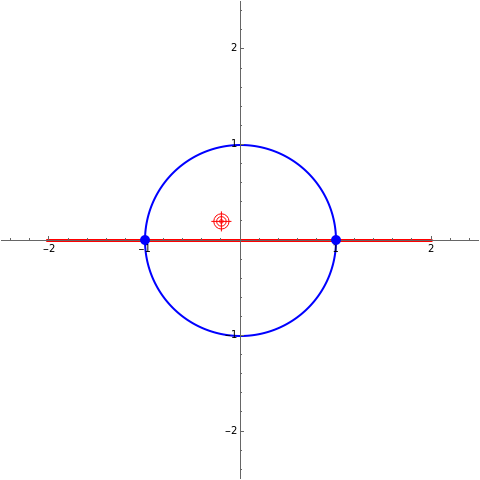
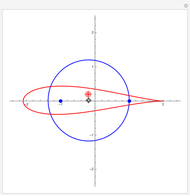
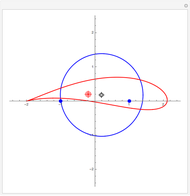
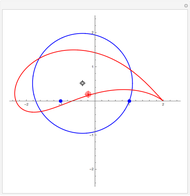
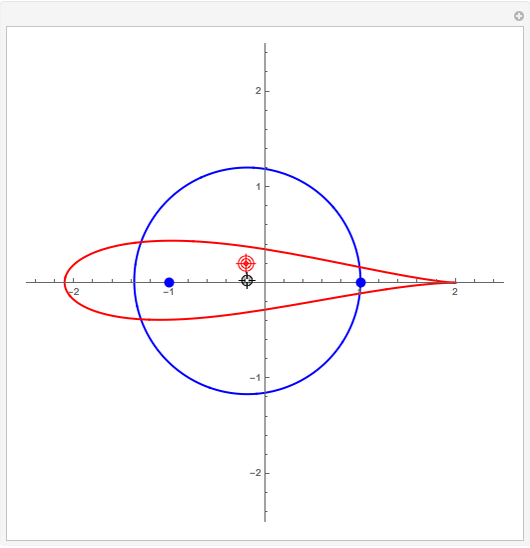
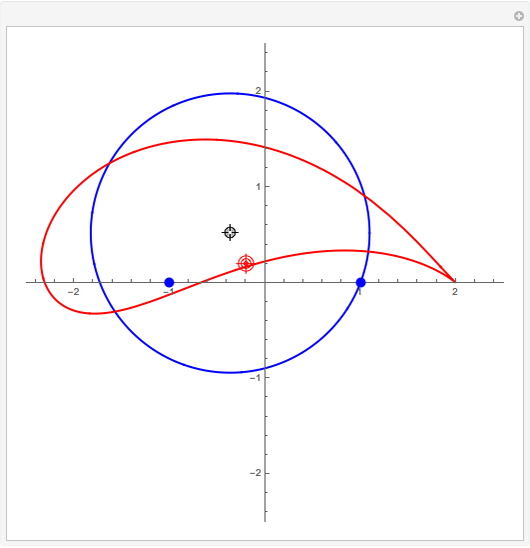
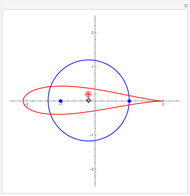
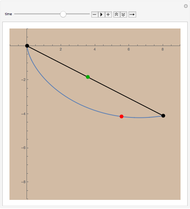
A simple way of modelling the cross section of an airfoil (or aerofoil) is to transform a circle in the Argand diagram using the Joukowski mapping, 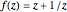 . The map is conformal except at the points
. The map is conformal except at the points 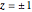 , where the complex derivative is zero. You can drag the circle's center to give a variety of airfoil shapes, but it should pass through one of these points and either pass through or enclose the other. In this Demonstration, a good result may be obtained by dragging the center of the circle to the red target at
, where the complex derivative is zero. You can drag the circle's center to give a variety of airfoil shapes, but it should pass through one of these points and either pass through or enclose the other. In this Demonstration, a good result may be obtained by dragging the center of the circle to the red target at 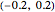 .
.
Contributed by: Phil Ramsden (December 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
If the center of the circle is at the origin, the image is not an airfoil but a line segment. For all other choices of center, the circle passes through one point at which the mapping fails to be conformal and encloses the other. This means the mapping is conformal everywhere in the exterior of the circle, so we can model the airflow across an cylinder using a complex analytic potential and then conformally transform to the airflow across an airfoil. The fact that the circle passes through exactly one of these two points means that the image has exactly one cusp and is smooth everywhere else.
Permanent Citation