The Law of Corresponding States for Hydrocarbons: the Two-Phase Region

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Consider the following six chemical species: ethane, propane, 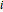 -butane,
-butane,  -butane,
-butane,  -pentane, and
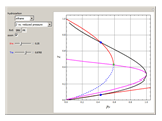
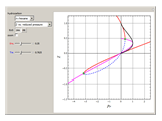
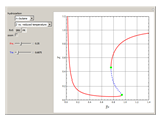
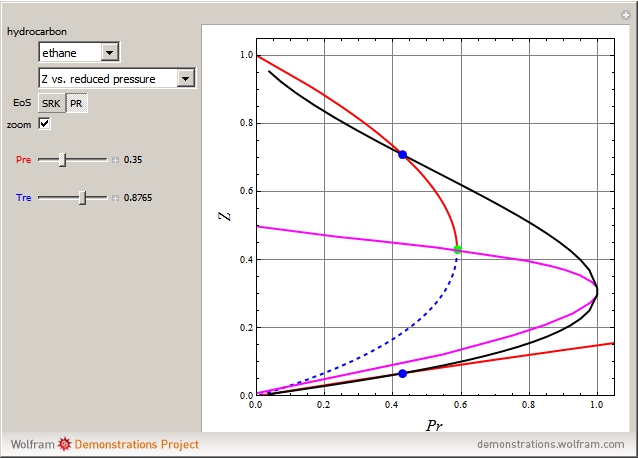
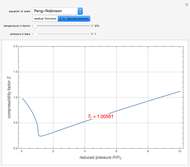
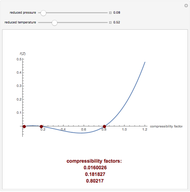
-pentane, and  -hexane. For each compound, this Demonstration uses arc-length continuation to plot (1) the compressibility factor
-hexane. For each compound, this Demonstration uses arc-length continuation to plot (1) the compressibility factor  versus reduced temperature
versus reduced temperature 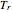 for user-set values of the reduced pressure
for user-set values of the reduced pressure  , or (2) the compressibility factor
, or (2) the compressibility factor  versus reduced pressure
versus reduced pressure 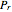 for user-set values of the reduced temperature
for user-set values of the reduced temperature 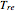 . You can choose between two equations of state for EOS; namely the Soave–Redlich–Kwong EOS or the Peng–Robinson EOS (see the Details section).
. You can choose between two equations of state for EOS; namely the Soave–Redlich–Kwong EOS or the Peng–Robinson EOS (see the Details section).
Contributed by: Housam Binous, Nayef M. Alsaifi, Ali Kh. Al-Matar, and Brian G. Higgins (April 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In the Soave–Redlich–Kwong (SRK) equation of state, the compressibility factor occurs as a solution of the cubic equation
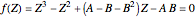 ,
,
where 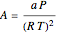 and
and  , with
, with  ,
, 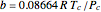 ,
, 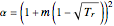 , and
, and 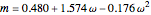 .
.
In the Peng–Robinson (PR) equation of state, the compressibility factor occurs as a solution of the cubic equation
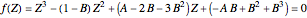 ,
,
where 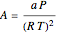 and
and  , with
, with  ,
, 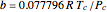 ,
, 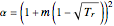 , and
, and 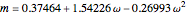 .
.
In the equations given above,  is the acentric factor,
is the acentric factor, 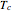 and
and 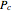 are the critical temperature and pressure, and
are the critical temperature and pressure, and 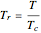 is the reduced pressure.
is the reduced pressure.
Reference
[1] W.-G. Dong and J. H. Lienhard, "Corresponding States Correlation of Saturated and Metastable Properties," The Canadian Journal of Chemical Engineering, 64(1), 1986 pp. 158–161. doi:10.1002/cjce.5450640123.
Permanent Citation