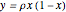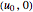The Logistic Difference Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The logistic difference equation (or logistic map)  , a nonlinear first-order recurrence relation, is a time-discrete analogue of the logistic differential equation,
, a nonlinear first-order recurrence relation, is a time-discrete analogue of the logistic differential equation,  . Like its continuous counterpart, it can be used to model the growth or decay of a process, population, or financial instrument.
. Like its continuous counterpart, it can be used to model the growth or decay of a process, population, or financial instrument.
Contributed by: Victor Hakim (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
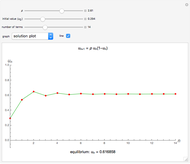
The equilibrium values for 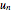 determine how or whether the long-term activity of a solution is predictable. If
determine how or whether the long-term activity of a solution is predictable. If  and
and 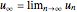 , then
, then 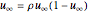 , and the equilibrium solutions are
, and the equilibrium solutions are  or
or  . Further investigation can be done to show that if
. Further investigation can be done to show that if 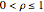 , then
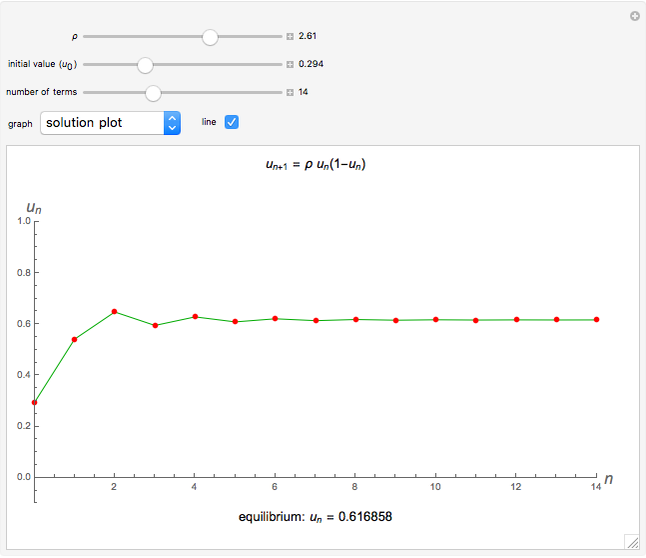
, then  is an asymptotically stable value. For
is an asymptotically stable value. For  , solutions converge instead to
, solutions converge instead to  . For
. For  , solutions do not converge to a fixed point, except when
, solutions do not converge to a fixed point, except when 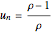 exactly for some
exactly for some 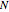 , in which case
, in which case 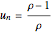 for all
for all  .
.
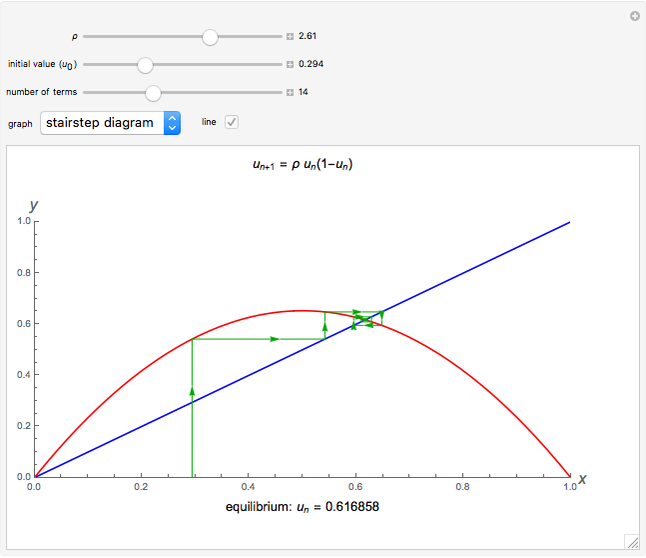
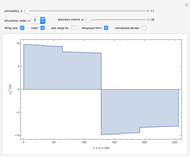
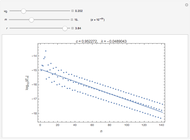
Snapshot 1: the solution converges to a single value
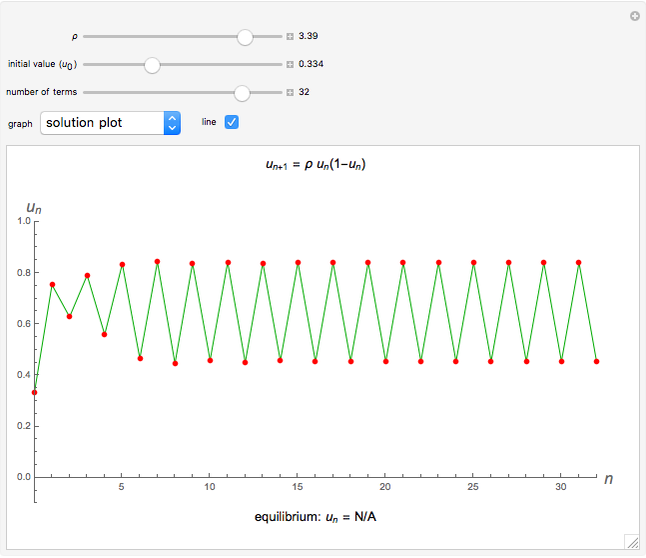
Snapshot 3: where  , the solution oscillates with period 2 (a "two-cycle")
, the solution oscillates with period 2 (a "two-cycle")
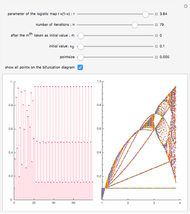
For larger values of  , the long-term activity is highly chaotic, though there may be certain values of
, the long-term activity is highly chaotic, though there may be certain values of  with oscillations of period 4, 8, 16, 32, … . In this chaotic region (
with oscillations of period 4, 8, 16, 32, … . In this chaotic region (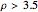 ), there is a high sensitivity to the value of
), there is a high sensitivity to the value of 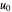 . Even varying
. Even varying 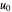 a small amount changes most terms drastically; the solution becomes unpredictable.
a small amount changes most terms drastically; the solution becomes unpredictable.
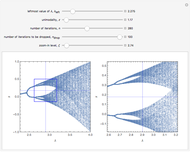
Snapshot 5: a solution that is chaotic and ultimately unpredictable; it can, however, be modeled as a simpler, three-cycle approximation
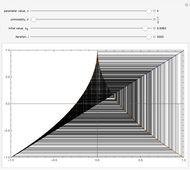
Snapshots 2, 4, and 6: the stairstep diagrams of snapshots 1, 3, and 5, respectively
Permanent Citation