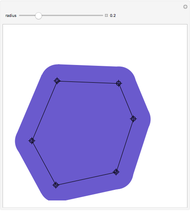
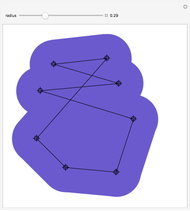
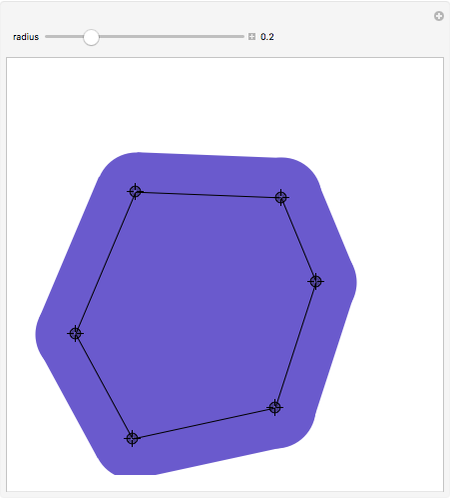
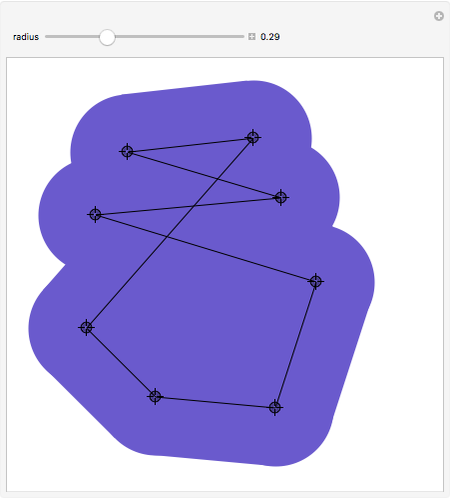
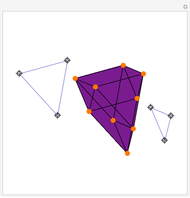
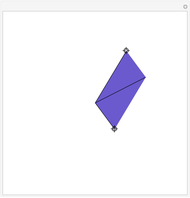
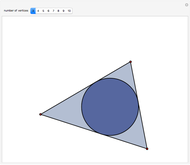
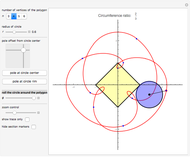
The Minkowski Sum of a Disk and a Polygon
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The Minkowski sum of two subsets in the plane,  and
and 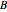 , is the set of all sums
, is the set of all sums 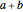 , where
, where 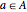 and
and 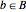 .
.
Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation