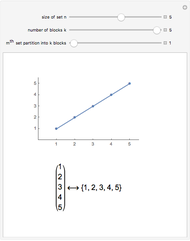
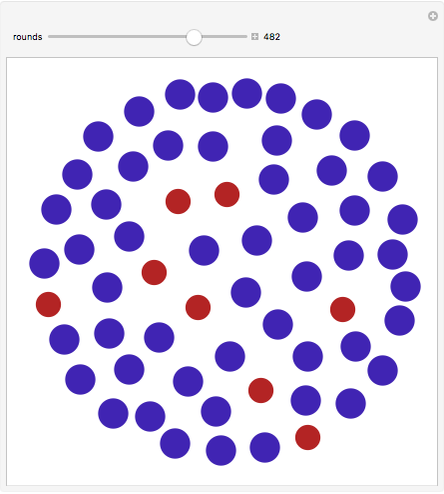
The Moran process is a simple stochastic model used to study evolution in finite populations. Consider a population of constant size with two types of individuals (e.g. "red" and "blue"). At each step a single individual is allowed to reproduce a clone of the same type. Furthermore, to keep population size constant, one individual has to die. Individuals for reproduction and elimination are chosen randomly. The types have different fitnesses that determine the rates at which they reproduce. If the fitness of type red is set to 1 and the fitness of type blue is set to , then the probability that type blue is chosen to reproduce is given by and the probability that type red is chosen to reproduce is given by 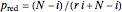. In this example, blue individuals have a relative fitness of 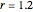and the point size is proportional to their relative fitness.