The Ontological Table

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
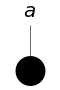
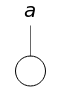
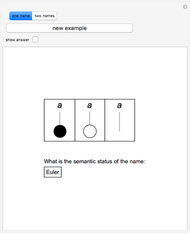
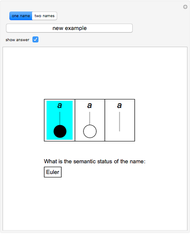
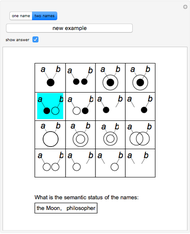
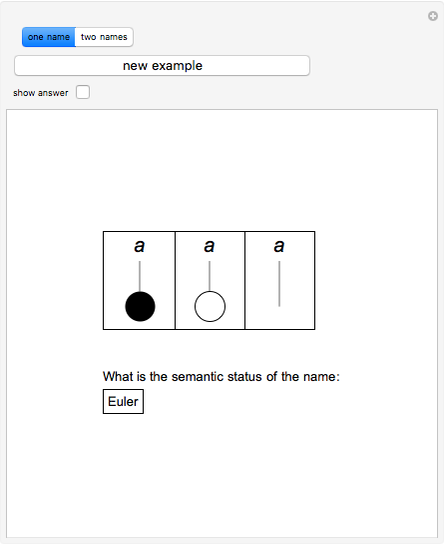
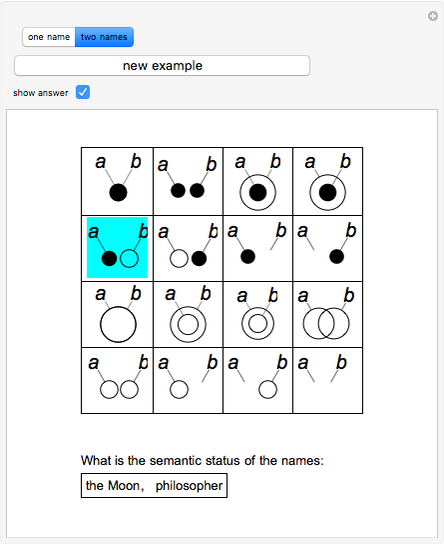
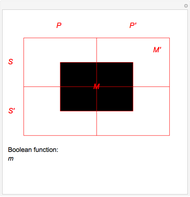
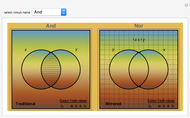
The ontological table is an extension of Euler's circles. Euler's circles do not take into account unshared names ("Socrates", "the Moon", ...) or fictitious names ("Pegasus", "centaur", ...). A black disk represents the only object named by an unshared name; a circle represents the many objects named by a shared name ("man", "philosopher", ...); no disk or circle is used in the case of a fictitious name. The ontological table consists of two subtables, for one name (3 diagrams) and for two names (16 diagrams).
[more]
Contributed by: Izidor Hafner (March 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The ontological table was introduced by Lejewski to give a visual way of explaining Leśniewski's ontology. It lets you determine the meaning of certain proposition-forming functors of one or two arguments that are names. Here are two examples:
The first functor of existence occurs in expressions of the type "there exists at least one  ." A proposition of this type is true if and only if one of the first two diagrams of the first table illustrates the semantic status of the name
." A proposition of this type is true if and only if one of the first two diagrams of the first table illustrates the semantic status of the name  .
.
The functor of singular inclusion occurs in expressions of the type " is
is  ." A proposition of this type is true if and only if the first or the third diagram of the second table illustrates the semantic status of the two names for which
." A proposition of this type is true if and only if the first or the third diagram of the second table illustrates the semantic status of the two names for which  and
and  stand.
stand.
For Euler's circles, see [2] or [3]. For more about Leśniewski's systems, see [4].
References
[1] C. Lejewski, "On Leśniewski's Ontology," in Leśniewski's Systems: Ontology and Mereology, The Hague: Martinus Nijhoff Publishers, 1984 pp. 123–148.
[2] E. J. Borowski and J. M. Borwein, Collins Dictionary of Mathematics, New York: HarperCollins Publishers, 1991 pp. 203.
[3] Wikipedia, "Euler Diagram." (Mar 18, 2016) en.wikipedia.org/wiki/Euler_diagram.
[4] Wikipedia, "Stanisław Leśniewski." (Mar 18, 2016) en.wikipedia.org/wiki/Stanis% C5 %82 aw_Le % C5 %9 Bniewski.
Permanent Citation