The Parrondo Paradox

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
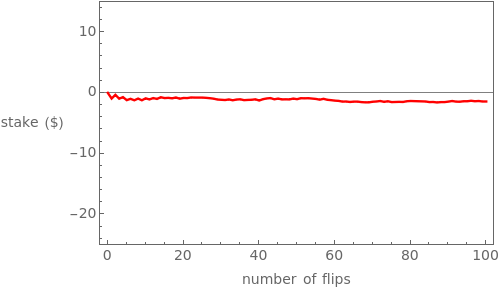
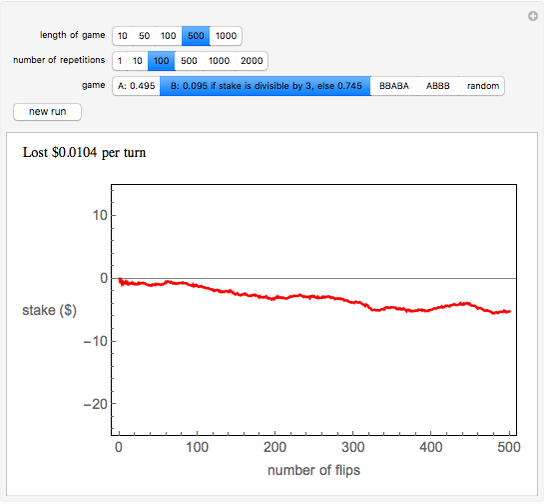
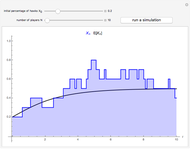
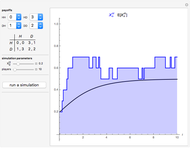
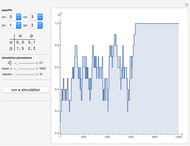
Parrondo's paradox is a surprising statement about the combination of certain probabilistic events. We start with two games A and B that, individually, are losing games. But we define game C as follows: Flip a fair coin and play A if the coin comes up heads and B if it comes up tails. Then C can be a winning game.
[more]
Contributed by: Stan Wagon (July 2011)
(Macalester College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
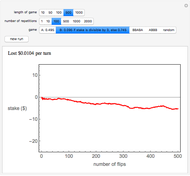
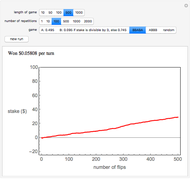
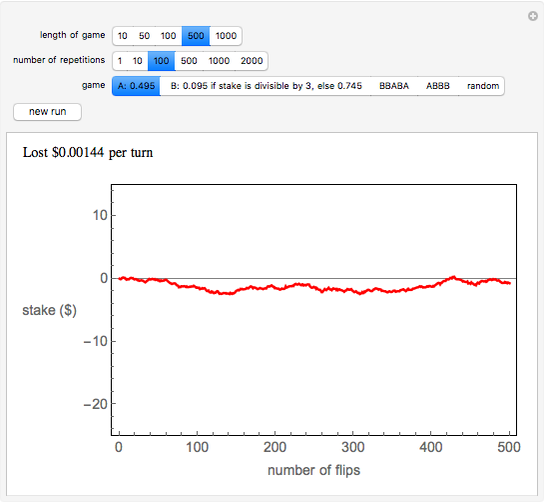
In the Demonstration, the lengths of the games are 500 flips and the results are averaged over 100 repetitions. Snapshots 1 and 2 show that games A and B are losing games. Snapshot 3 shows that the combination ABBAB is a winning game.
For more information on the paradox, which arose from some considerations of physics, see Parrondo's paradox or the MathWorld Parrondo's paradox (Wolfram MathWorld) entry. For detailed analysis of the games discussed here, see [1].
Reference
[1] D. Velleman and S. Wagon, "Parrondo's Paradox," Mathematica in Education and Research, 9(3–4), 2001 pp. 85–90.
Permanent Citation