Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Path of the Rear Wheels of a Bus

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

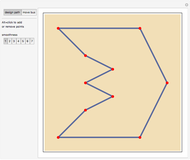
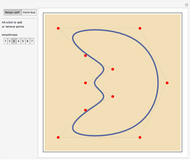
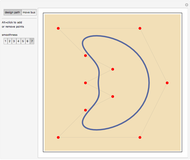
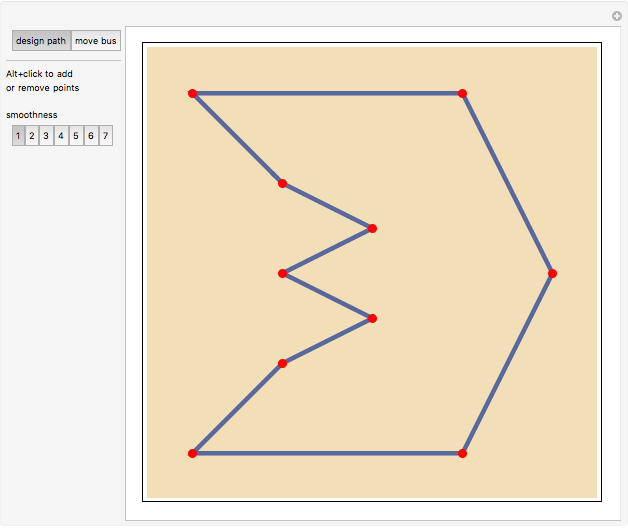
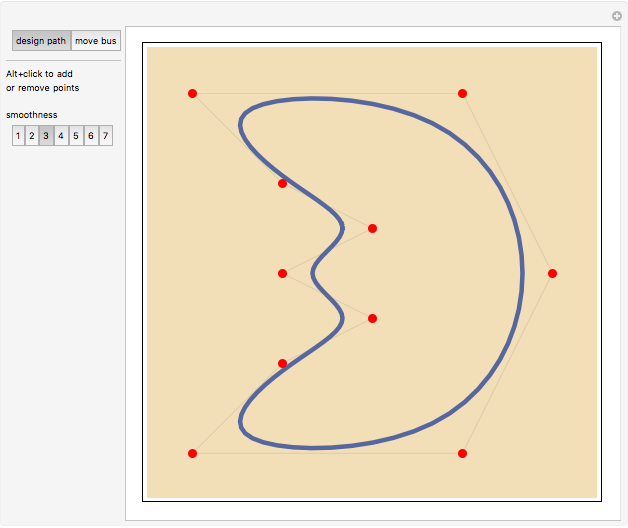
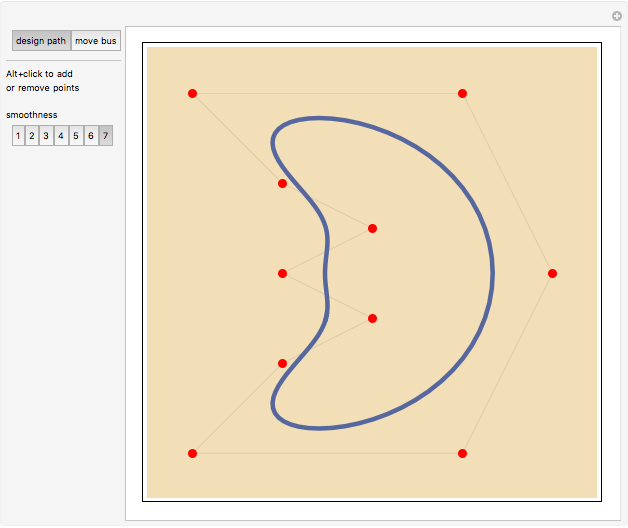
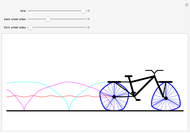
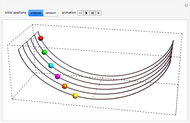
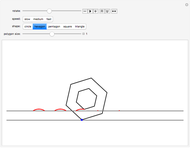
This Demonstration shows the path followed by the rear wheels of a bus as its front moves along a road. You can design the road using locators as control points for a closed spline and choosing its smoothness. You can drag the locators and you can create or eliminate them with Alt+click. Once designed, the path is used by the bus for a certain number of circuits.

[more]

The midpoint of the front of the bus (orange) moves along the blue path and the rear of the bus traces the thin black path. As the length of the bus increases, a variety of unpredictable patterns emerge, most of them having cusps, even though the front moves along a smooth curve. Sometimes the bus has to move in reverse.

[less]

Contributed by: Jaime Rangel-Mondragon (July 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] H. I. Feeman and S. D. Riemenschneidr, "Determining the Path of the Rear Wheels of a Bus," SIAM Review, 25, 1983 pp. 561–567.

[2] G. E. Prince and S. P. Dubois, "Mathematical Models for Motion of the Rear Ends of Vehicles," Mathematical and Computer Modelling, 49, 2009 pp. 2049–2060.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send