The Physics of Spiderman's Swing

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
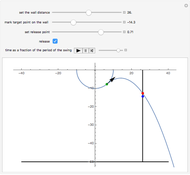
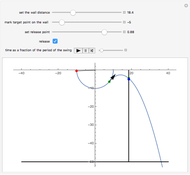
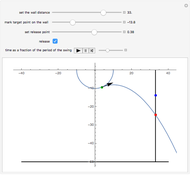
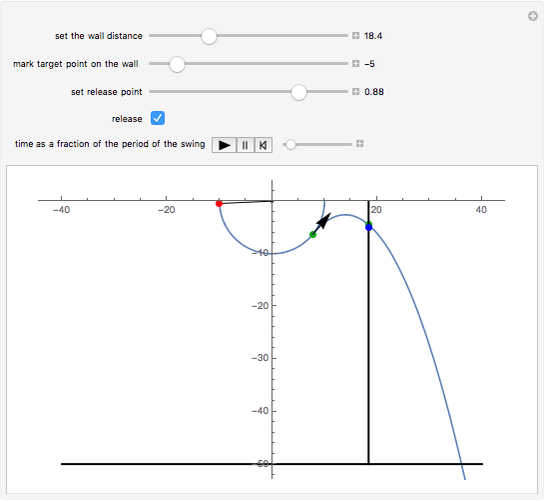
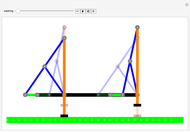
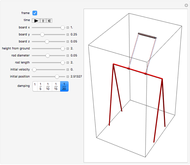
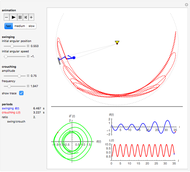
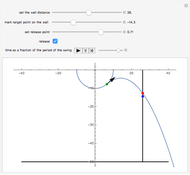
Can Spiderman land at the blue mark?
[more]
Contributed by: Stelios Kapranidis and Ron Ruszczyk (April 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
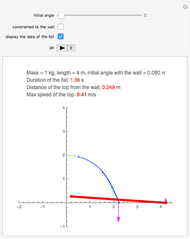
The motion of the pendulum of length 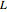 can be determined by using the principle of conservation of mechanical energy
can be determined by using the principle of conservation of mechanical energy
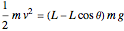 ,
,
which gives
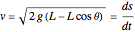 .
.
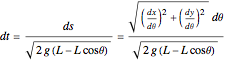 .
.
The solution of this differential equation 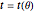 gives the time it takes the pendulum to reach a position
gives the time it takes the pendulum to reach a position  . Using the inverse of this function,
. Using the inverse of this function, 
 , we find the position of the pendulum at time
, we find the position of the pendulum at time  as
as
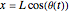 ,
,
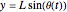 .
.
When the bob is released at time  at position
at position 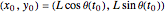 , the projectile motion of the bob is given by the equations
, the projectile motion of the bob is given by the equations
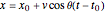 ,
,
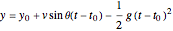 ,
,
where the velocity 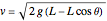 .
.
Permanent Citation