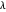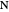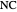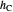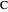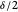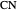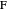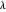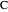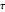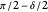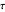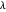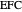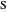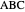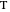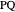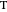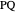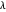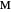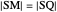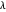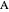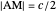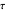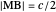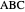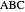Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Plemelj Construction of a Triangle: 14

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

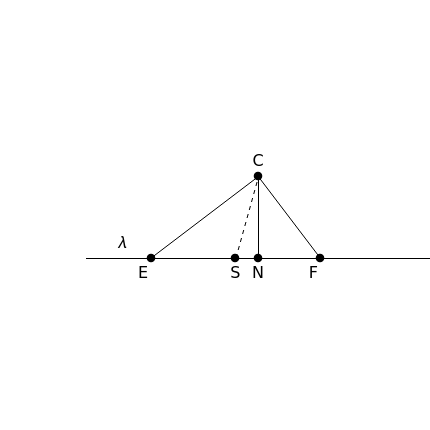
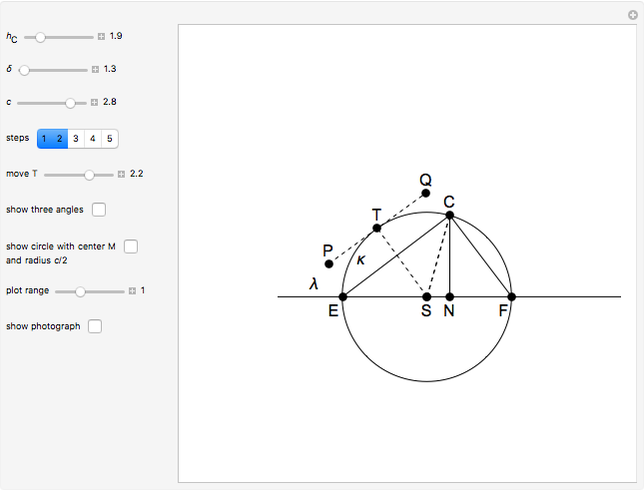
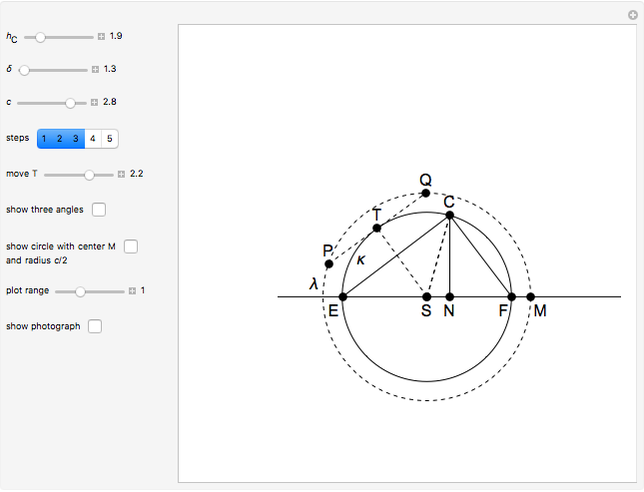
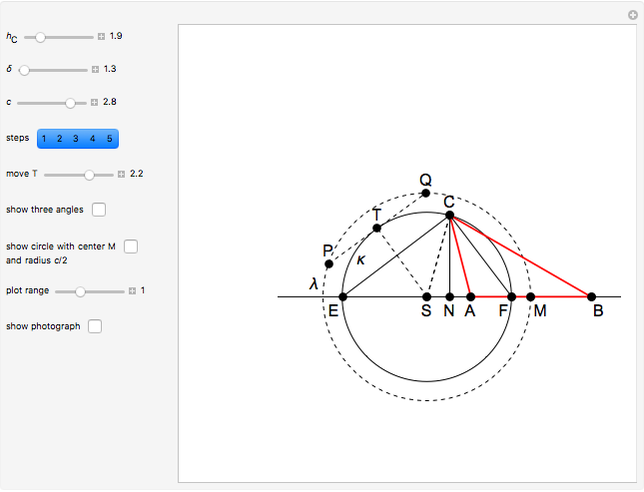
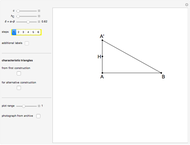
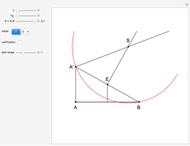
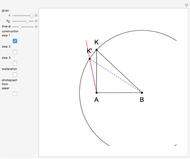
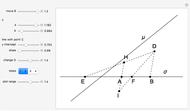
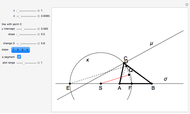
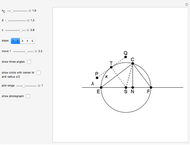
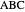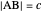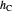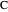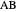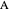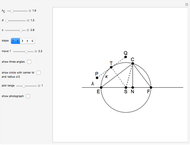
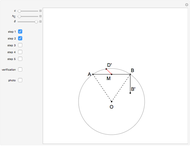
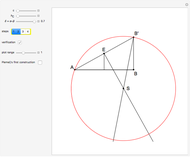
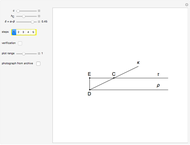
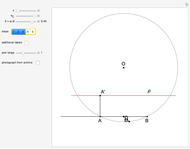
The problem is to construct a triangle given the length of its base, the length of the altitude from to and the difference of the angles at and 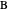. This Demonstration shows Gerd Baron's solution of this construction problem using the Apollonius circle.

[more]

Construction

Step 1: On line , choose a point . Draw a vertical segment of length . From , draw a ray at angle with respect to the segment . Let be the intersection of the ray and . From , draw a ray at angle and opposite to with respect to the segment . Let be the intersection of the ray and . The triangle is right angled. Let be the midpoint of .

Step 2: Draw a circumcircle of the triangle with center . This circle is the Apollonius circle of the triangle . Choose any point on the circle and draw a tangent of length with as the midpoint of .

Step 3: On , draw a point such that .

Step 4: On , draw the point so that . On , measure out the point so that .

Step 5: The triangle meets the stated conditions.

Verification

The correctness of the construction follows from properties of the Apollonius circle of the triangle . The radius of the Apollonius circle is and is independent of .

[less]

Contributed by: Gerd Baron, Izidor Hafner, Marko Razpet and Nada Razpet (August 2018)
Open content licensed under CC BY-NC-SA

Snapshots

Details

As far we know, this problem first appeared in [1]. The problem was also posed by Stevens in [2].

The photograph of Stevens's solution was taken from [2, Vol. VI, 1857 p. 56].

For the history of Plemelj's solutions of this problem, see The Plemelj Construction of a Triangle: 1.

References

[1] L. H. von Holleben and P. Gerwien, Aufgaben-Systeme und Sammlungen aus der Ebenen Geometrie: Aufgaben, Berlin: G. Reimer, 1832.

[2] The Ohio Journal of Education, (4), 1855 pp. 278 and 369; (5), 1856 p. 112; (6), 1857 pp. 56–57, 145 and 184.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send