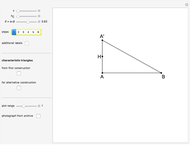
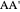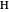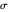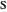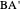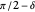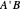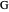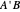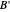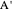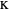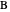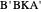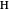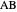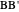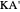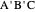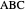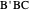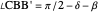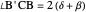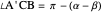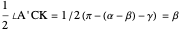The Plemelj Construction of a Triangle: 7
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
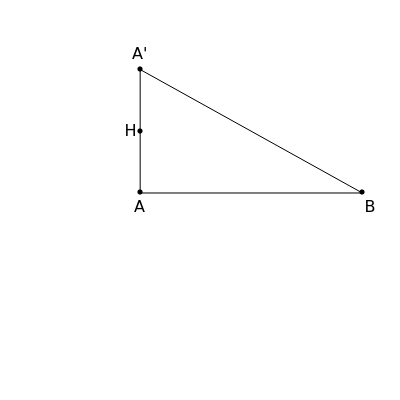
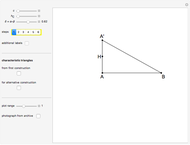
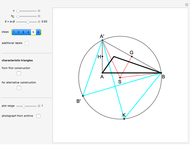
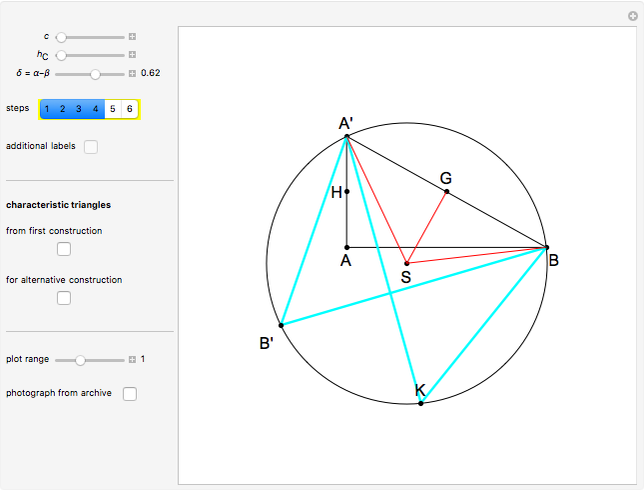
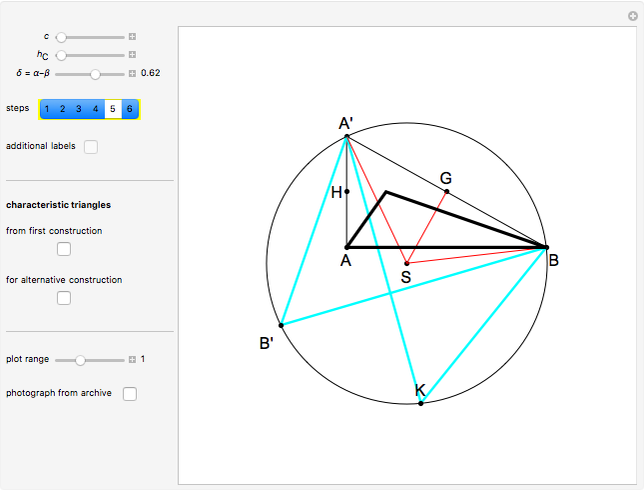
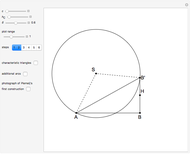
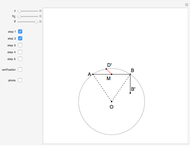
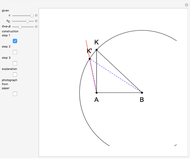
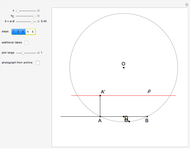
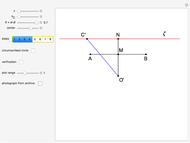
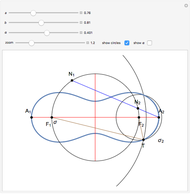
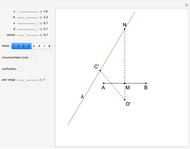
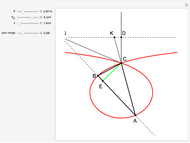
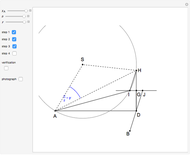
This Demonstration constructs a triangle  given the length
given the length 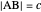 of its base, the length
of its base, the length  of the altitude from
of the altitude from 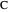 to
to 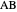 and the difference
and the difference  between the angles at
between the angles at 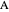 and
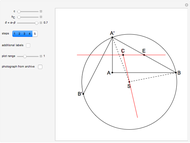
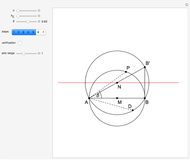
and 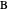 . This is not Plemelj's construction, but a new one that unifies Plemelj's first construction and an alternative one.
. This is not Plemelj's construction, but a new one that unifies Plemelj's first construction and an alternative one.
Contributed by: Izidor Hafner, Nada Razpet and Marko Razpet (August 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the history of this problem, references and a photograph of Plemelj's first solution, see The Plemelj Construction of a Triangle: 1.
Permanent Citation