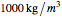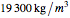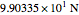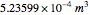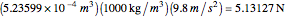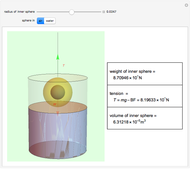
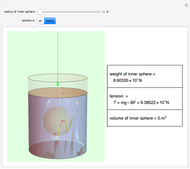
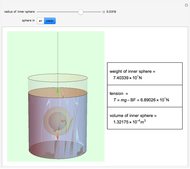
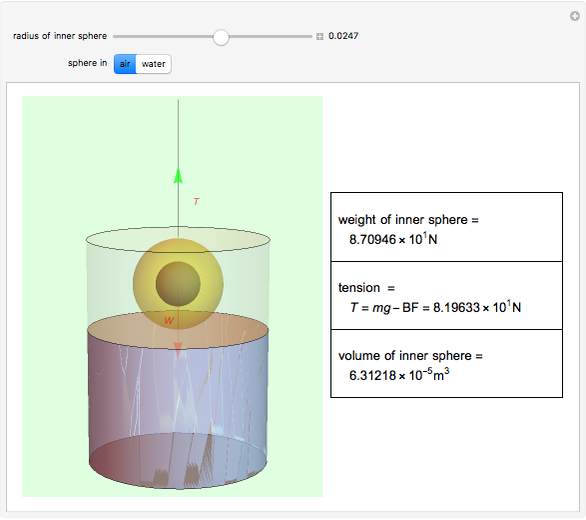
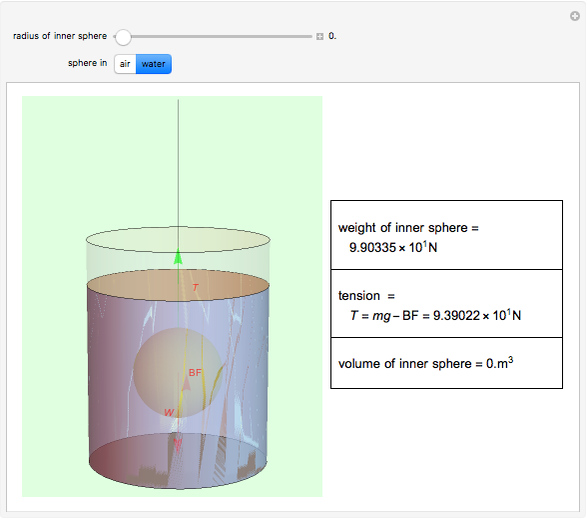
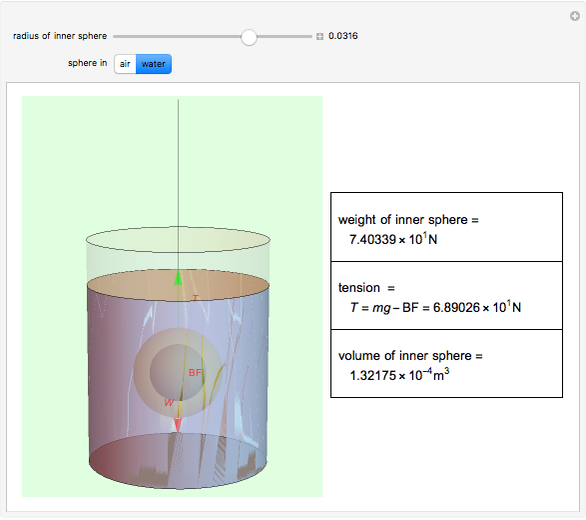
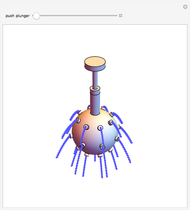
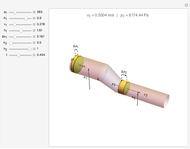
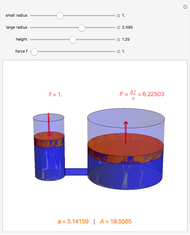
A gold sphere is submerged in water. It is suspected that the center might be empty or made of some lighter material. According to Archimedes's principle, we can determine the volume of the inner sphere by measuring the difference between the weight of the entire sphere in and out of water; that difference must be equal to the buoyant force, the weight of the volume of water displaced. Then the difference between the volume of gold in the hollowed sphere and the volume of the water displaced equals the volume of the inner sphere.