The Quantum Harmonic Oscillator with Time-Dependent Boundary Condition in the Causal Interpretation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
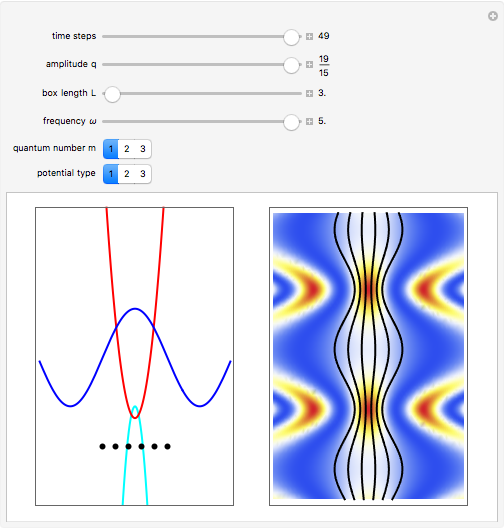
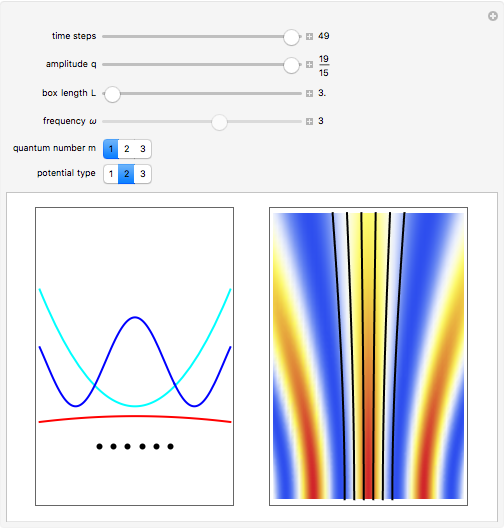
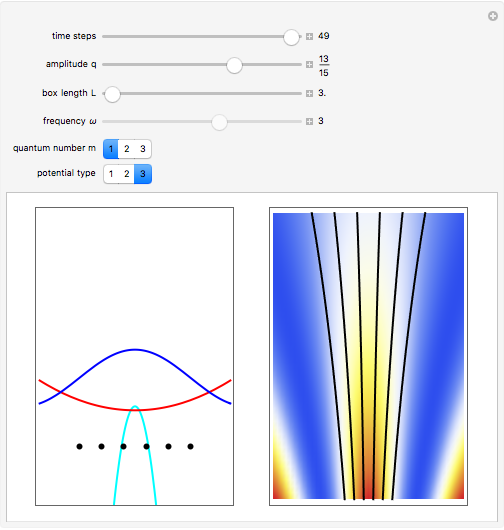
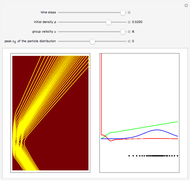
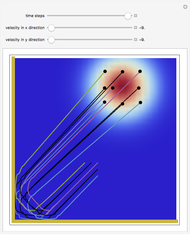
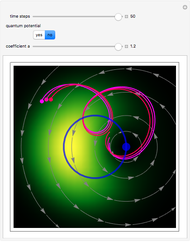
One of the challenging aspects of quantum mechanics is to derive the classical world from the quantum world. In this Demonstration, we discuss the dynamics of quantum particles bouncing between two oscillating infinitely high walls. The shape of the bottom of the well is described by a harmonic oscillator potential with a time-dependent frequency  . In the causal approach, the quantum potential governs the dynamics of the quantum particle; the link between classical Newtonian mechanics and the quantum world is the quantum potential. The total effective potential is the sum of the potential
. In the causal approach, the quantum potential governs the dynamics of the quantum particle; the link between classical Newtonian mechanics and the quantum world is the quantum potential. The total effective potential is the sum of the potential 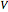 and the quantum potential (
and the quantum potential (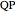 ), which leads to the time-dependent quantum force. In a single nonstationary state the quantum particles in the ensemble therefore behave classically in spite of having an associated wave function that satisfies the Schrödinger equation.
), which leads to the time-dependent quantum force. In a single nonstationary state the quantum particles in the ensemble therefore behave classically in spite of having an associated wave function that satisfies the Schrödinger equation.
Contributed by: Klaus von Bloh (March 2011)
Open content licensed under CC BY-NC-SA
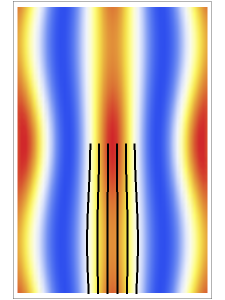
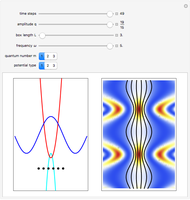
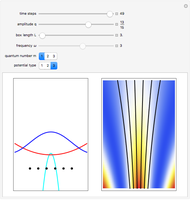
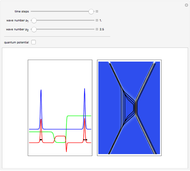
Snapshots
Details
Exact nontrivial analytic solutions of the trajectory equation in the Bohm approach can be found only for a very limited number of cases. Fortunately, for a single nonstationary state, an analytical solution exists for the trajectories in both the classical and quantum treatments. In this special case, the classical and the quantum trajectories are the same (up to a constant factor), because the quantum potential 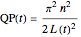 has a space-independent amplitude. The wavefunction obeys the Schrödinger equation
has a space-independent amplitude. The wavefunction obeys the Schrödinger equation 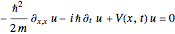 with the potential term
with the potential term 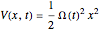 . The auxiliary function
. The auxiliary function 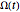 is defined by
is defined by 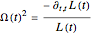 , from which the analytical wavefunction is given by
, from which the analytical wavefunction is given by 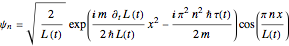 , with
, with  , where
, where 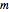 is the mass and
is the mass and 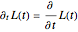 , and so on. The function
, and so on. The function 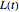 is the time-dependent length of the moving walls,
is the time-dependent length of the moving walls, 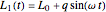 ,
, 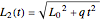 ,
, 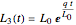 , with the initial width
, with the initial width 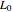 , the amplitude
, the amplitude  , and the frequency
, and the frequency  . In the quantum case, the analytical solution for the quantum trajectories is derived from the phase of the wavefunction in the eikonal form:
. In the quantum case, the analytical solution for the quantum trajectories is derived from the phase of the wavefunction in the eikonal form:  . Therefore, the equation for the quantum trajectory with
. Therefore, the equation for the quantum trajectory with 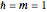 is given by
is given by 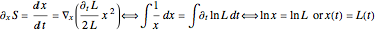 .
.
Reference
[1] A. J. Makowski and P. Peplowski, "On the Behaviour of Quantum Systems with Time-Dependent Boundary Conditions," Physics Letters A 163(3), 1992 pp. 143–151.
Permanent Citation