The Size of an Automorphism Group

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration expresses a multiplicative unit group modulo an integer in terms of isomorphic additive groups and then uses the additive groups to compute the total number of automorphisms of the unit group.
Contributed by: Dominic Milioto (June 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
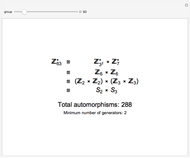
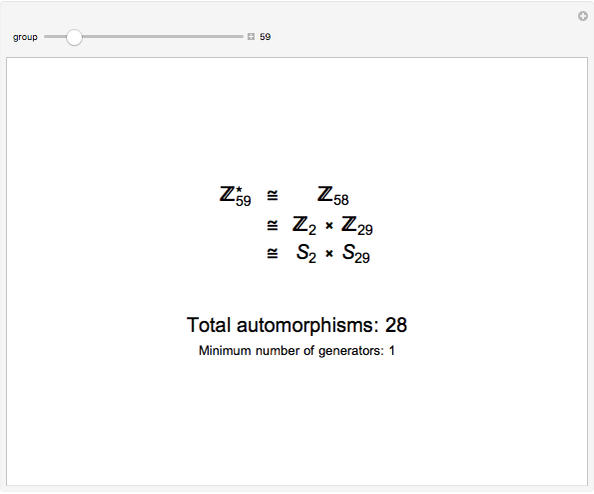
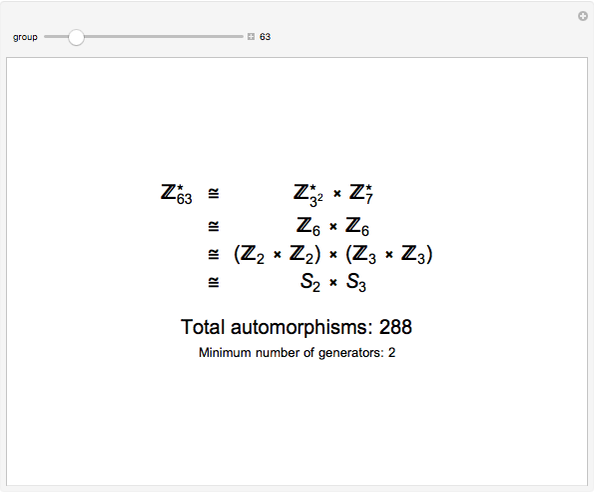
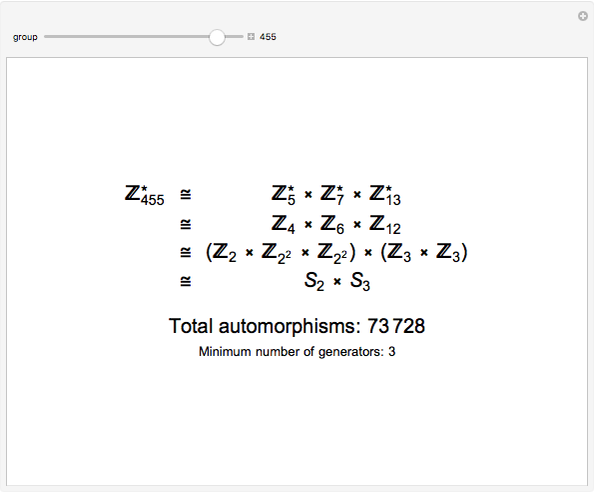
In this Demonstration, 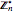 represents the multiplicative unit group of integers modulo
represents the multiplicative unit group of integers modulo  , and
, and 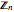 represents the additive group of integers mod
represents the additive group of integers mod  .
.
If 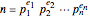 , then
, then  . Each
. Each 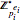 is isomorphic to an additive group according to the following rules:
is isomorphic to an additive group according to the following rules:  ,
, 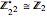 , and
, and 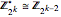 for
for  ; and for odd prime
; and for odd prime 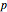 ,
,  . These isomorphisms can be derived by using the Euler totient function,
. These isomorphisms can be derived by using the Euler totient function, 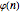 , which gives the number of positive integers less than or equal to
, which gives the number of positive integers less than or equal to  that are relatively prime to
that are relatively prime to  . For example, consider
. For example, consider 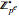 for odd
for odd 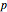 . We have
. We have 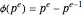 and therefore
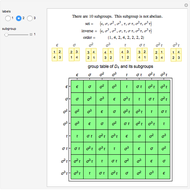
and therefore  , since both groups are cyclic and of the same order. Once the group has been factored into additive groups, the groups are combined according to prime powers. Each prime power set is a Sylow
, since both groups are cyclic and of the same order. Once the group has been factored into additive groups, the groups are combined according to prime powers. Each prime power set is a Sylow 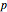 -group,
-group, 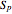 , and these allow the easy determination of
, and these allow the easy determination of 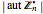 according to the formula:
according to the formula:
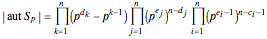 with
with 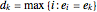 and
and 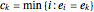 .
.
Any Abelian group such as 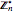 is isomorphic to a product of Sylow
is isomorphic to a product of Sylow 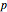 -groups, and the number of automorphisms of
-groups, and the number of automorphisms of 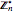 is a product of the number of automorphisms of its Sylow
is a product of the number of automorphisms of its Sylow 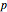 -groups.
-groups.
In the case of  , we have
, we have 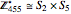 . For
. For 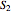 , the exponents are
, the exponents are  ,
,  , and
, and  , with
, with 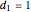 ,
,  ,
,  , and
, and  ,
, 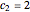 ,
, 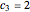 .
.
This gives 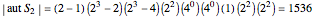 .
.
A similar calculation gives 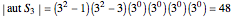 .
.
Therefore 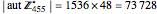 .
.
By considering the generators needed to generate the Cartesian product  , it can be shown that the minimum number of generators needed to generate
, it can be shown that the minimum number of generators needed to generate 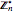 is simply the number of factors of the Sylow 2-group. The last line of the result reports this number.
is simply the number of factors of the Sylow 2-group. The last line of the result reports this number.
For more details and a derivation of the formula above, see [1].
Reference
[1] C. J. Hillard and D. L. Rhea. "Automorphisms of Finite Abelian Groups". www.msri.org/people/members/chillar/files/autabeliangrps.pdf.
Permanent Citation