The Structure of the Real Roots of a Quintic Polynomial

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
For any polynomial 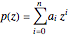 , the discriminant of
, the discriminant of  is a polynomial in the coefficients
is a polynomial in the coefficients 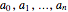 which is zero only when
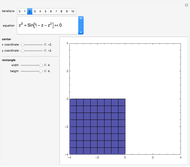
which is zero only when  has multiple roots. However, the complete root structure of a general polynomial (i.e., the conditions that the coefficients must satisfy in order that the polynomial has a specified number of single, double, or multiple roots) is much harder to determine. Here we show graphically the solution of the problem for a polynomial of degree five of the form
has multiple roots. However, the complete root structure of a general polynomial (i.e., the conditions that the coefficients must satisfy in order that the polynomial has a specified number of single, double, or multiple roots) is much harder to determine. Here we show graphically the solution of the problem for a polynomial of degree five of the form 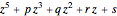 , where all the coefficients are real. We regard
, where all the coefficients are real. We regard  as coordinates of a point in the unit cube of length 10, with center at the origin. The constant coefficient
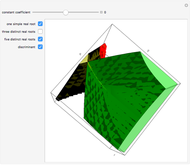
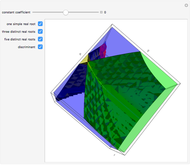
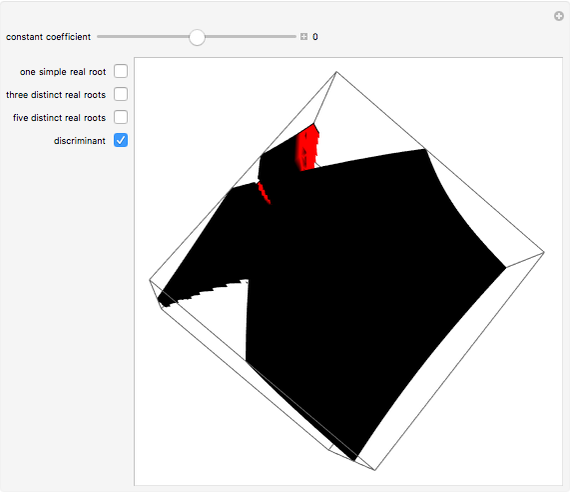
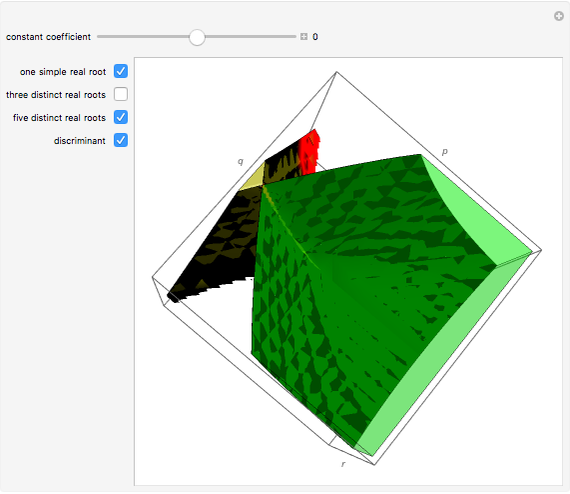
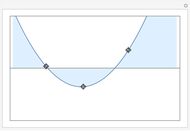
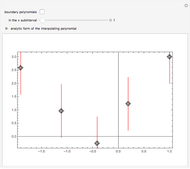
as coordinates of a point in the unit cube of length 10, with center at the origin. The constant coefficient  , initially set to 0, can be varied by means of a slider taking values between -5 and 5. The parts of the cube corresponding to polynomials with a simple real root, three distinct real roots, five distinct real roots, and the discriminant are shown in different colors. The discriminant (the part of the cube corresponding to polynomials with multiple, possibly complex, roots) is also shown. The part of the discriminant colored red corresponds to polynomials with exactly four distinct real roots (one of them a double root); the rest of the discriminant is colored black. Note that the discriminant is not disjoint from the other areas shown, since a polynomial can have (for example) a simple real root and a double complex one, thus lying both on the discriminant and in the green area. To give the complete decomposition of the cube, the black part of the discriminant would have to be partitioned further, corresponding to different multiplicity structures of roots. This has been done algebraically (see the Details section) but is difficult to represent graphically so it is not done here.
, initially set to 0, can be varied by means of a slider taking values between -5 and 5. The parts of the cube corresponding to polynomials with a simple real root, three distinct real roots, five distinct real roots, and the discriminant are shown in different colors. The discriminant (the part of the cube corresponding to polynomials with multiple, possibly complex, roots) is also shown. The part of the discriminant colored red corresponds to polynomials with exactly four distinct real roots (one of them a double root); the rest of the discriminant is colored black. Note that the discriminant is not disjoint from the other areas shown, since a polynomial can have (for example) a simple real root and a double complex one, thus lying both on the discriminant and in the green area. To give the complete decomposition of the cube, the black part of the discriminant would have to be partitioned further, corresponding to different multiplicity structures of roots. This has been done algebraically (see the Details section) but is difficult to represent graphically so it is not done here.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The problem of finding the number of real roots of a real polynomial and determining their multiplicities has a long history, going back at least to the 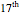 century and Descartes's law of signs. In the case when the coefficients are numeric there are several well-known ways of solving the problem (see [1]). However, for polynomials with symbolic coefficients the problem was completely solved only relatively recently [2], in which the authors describe an algorithm that for any polynomial with real symbolic coefficients determines the conditions for the number of roots and their multiplicity to be of a specified type. This Demonstration is based on an application of this algorithm to a quintic polynomial with symbolic roots given in [3].
century and Descartes's law of signs. In the case when the coefficients are numeric there are several well-known ways of solving the problem (see [1]). However, for polynomials with symbolic coefficients the problem was completely solved only relatively recently [2], in which the authors describe an algorithm that for any polynomial with real symbolic coefficients determines the conditions for the number of roots and their multiplicity to be of a specified type. This Demonstration is based on an application of this algorithm to a quintic polynomial with symbolic roots given in [3].
[1] S. Basu, R. Pollack, and M-F. Roy, Algorithms in Real Algebraic Geometry, Berlin: Springer, 2003.
[2] L. Yang, X. Hou, and Z. B. Zeng, "A Complete Discrimination System for Polynomials," Science in China, Ser. E 39(6), 1996 pp. 628–646.
[3] L. Yang and B. Xia, "An Explicit Criterion to Determine the Number of Roots in an Interval of a Polynomial," Progr. in Nat. Sci., 10(12), 2000 pp. 897–910.
Permanent Citation