The Thomson Problem with Central Forces

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
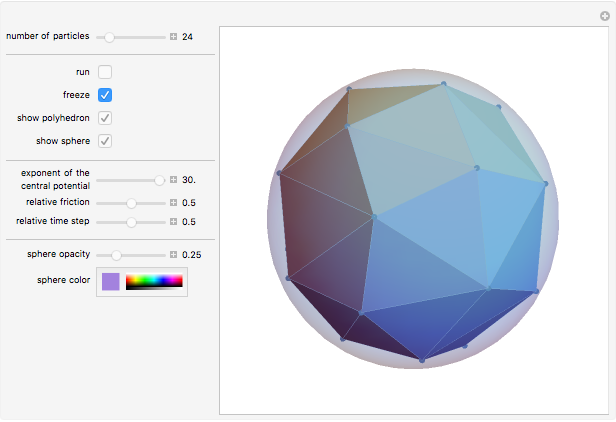
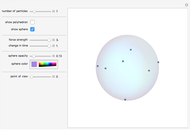
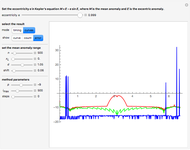
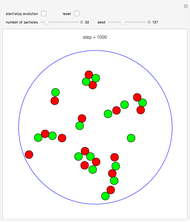
The Thomson problem concerns the equilibrium positions of  identical point charges constrained to move, without friction, on the surface of a sphere. Instead of motion constrained to a sphere, we consider motion in a central field with varying exponents, produced by a spherically symmetric charge density inside the sphere, with a total charge opposite to that of the point particles. For the case of a constant charge density in the sphere, the default setting, this is exactly the configuration that Thomson studied as a model for atoms (the plum pudding model), which suggested the present problem. The equilibrium positions are found here by the relaxation method—that is, by friction-damped motion from random stationary initial positions of the particles. Remarkably, the particles find their final resting positions on a spherical surface, although a naive expectation might favor a configuration with differing radial positions.
identical point charges constrained to move, without friction, on the surface of a sphere. Instead of motion constrained to a sphere, we consider motion in a central field with varying exponents, produced by a spherically symmetric charge density inside the sphere, with a total charge opposite to that of the point particles. For the case of a constant charge density in the sphere, the default setting, this is exactly the configuration that Thomson studied as a model for atoms (the plum pudding model), which suggested the present problem. The equilibrium positions are found here by the relaxation method—that is, by friction-damped motion from random stationary initial positions of the particles. Remarkably, the particles find their final resting positions on a spherical surface, although a naive expectation might favor a configuration with differing radial positions.
Contributed by: Ulrich Mutze (September 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
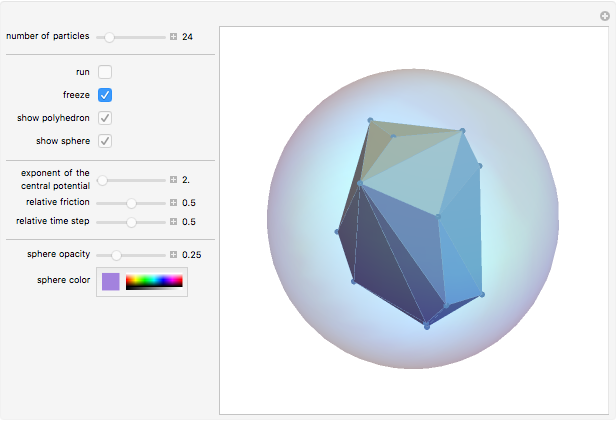
Snapshot 1: an initial random configuration of particles
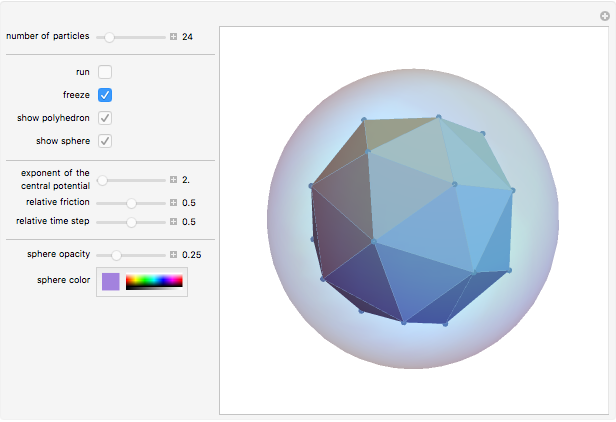
Snapshot 2: the final configuration after having come to rest in the default force field
Snapshot 3: the final configuration for a force field made by a positive space charge concentrated near the surface of the sphere
Snapshot 4: final configuration for a large number of particles
Snapshot 5: view with the sphere made transparent
Snapshot 6: view with the polyhedron removed from the particles
Snapshot 7: a non-default configuration not yet having come to rest
This Demonstration owes many coding details to the Demonstration "Repulsionhedra and the Thomson Problem" by Brian Burns.
The nature of energy minima at the equilibrium positions is studied in the Demonstration "Visualizing the Thomson Problem" by Mark Peterson.
Permanent Citation