Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

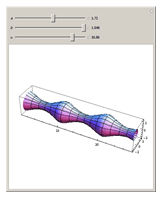
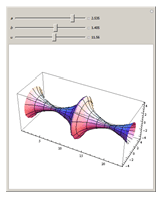
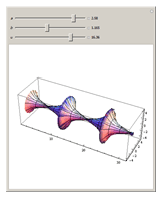
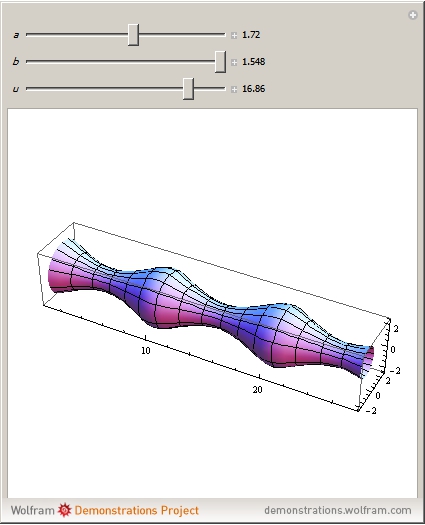
The Unduloid

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

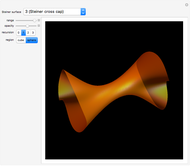
First studied by Delaunay [1], the unduloid (or onduloid) is a surface of revolution of an elliptic catenary with constant nonzero mean curvature (in this case, the reciprocal of twice the major axis length, 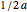). It can be obtained by tracing the focus of a rolling ellipse along a fixed line. This surface appears in fields like string theory [2] and carbon nanotubes [3].

Contributed by: Enrique Zeleny (May 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The unduloid is the solution of the differential equation

,

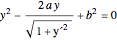where and are constants.

A parametrization of an unduloid can be represented by

,

where

.

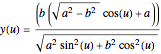References

[1] C. Delaunay, "Sur la surface de révolution dont la courbure moyenne est constante," Journal de Mathématiques Pures et Appliquées, 6, 1841 pp. 309–320. portail.mathdoc.fr/JMPA/afficher_notice.php?id=JMPA_ 1841_ 1_ 6_A24 _ 0.

[2] K. Maeda and U. Miyamoto, "Black Hole-Black String Phase Transitions from Hydrodynamics." arxiv:0811.2305.

[3] I. M. Mladenov, M. Ts. Hadzhilazova, V. M. Vassilev, and P. A. Djondjorov, "Unduloid-like Equilibrium Shapes of Carbon Nanotubes Subjected to Hydrostatic Pressure," Geometric Methods in Physics, Trends in Mathematics (P. Kielanowski, S. T. Ali, A. Odesskii, A. Odzijewicz, M. Schlichenmaier, and T. Voronov, eds.), Basel: Birkhauser, 2013 pp. 195–202. doi:10.1007/978-3-0348-0645-9_ 18.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send