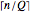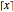The Vehicle Routing Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
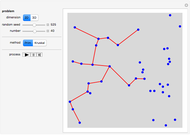
A special case of the general vehicle routing problem (VRP) is the school bus problem. Each bus has the same passenger capacity 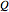 and a group of
and a group of  students is distributed in 2D; we seek a set of bus routes that minimizes the total distance traveled by the buses to pick up all the students. Each bus is assumed to start and finish at the school.
students is distributed in 2D; we seek a set of bus routes that minimizes the total distance traveled by the buses to pick up all the students. Each bus is assumed to start and finish at the school.
Contributed by: Stan Wagon and Yu Zhao (February 2013)
(Macalester College)
Open content licensed under CC BY-NC-SA
Snapshots
Details
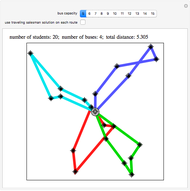
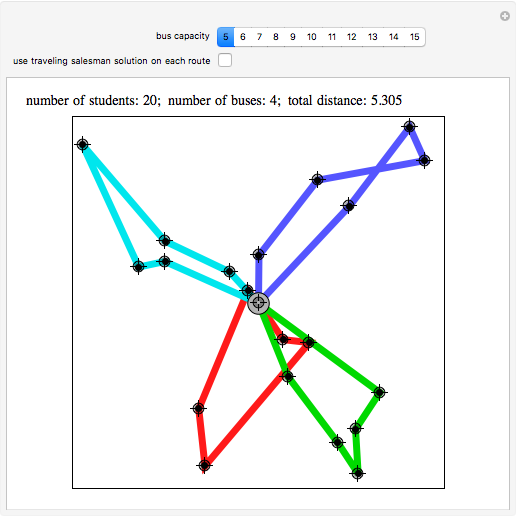
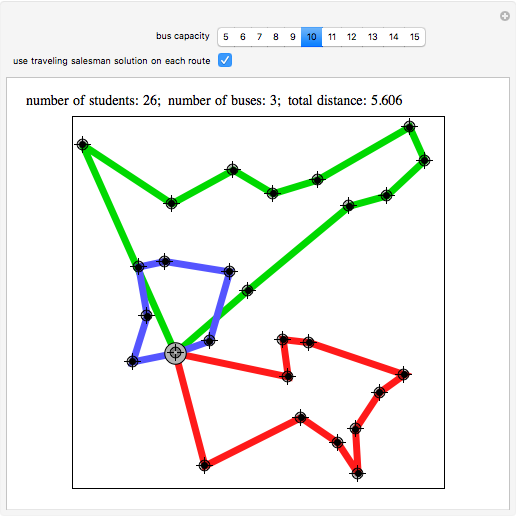
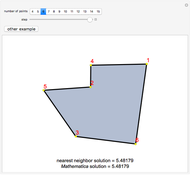
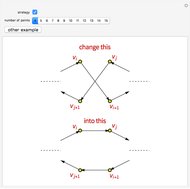
Details of the CW method can be found in [1]. A complication is that the method, which forms routes and merges them, might not end up with a solution that uses the minimal number of buses. For example, with 10 students and capacity 5, the method can end up with loads of size 4, 3, 3, and then no further merging will respect the capacity restraint. In this Demonstration we want to minimize the number of buses, and that is achieved by adding a small amount of randomization to CW and running it 10 times with such randomization in addition to once with no randomization. The random enhancement comes when routes are selected to be merged: instead of greedily choosing a merge with the largest savings, one can randomly choose between the two best. Then the least-cost solution is chosen from among those of the 11 solutions that use the minimum number of buses.
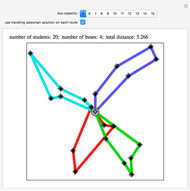
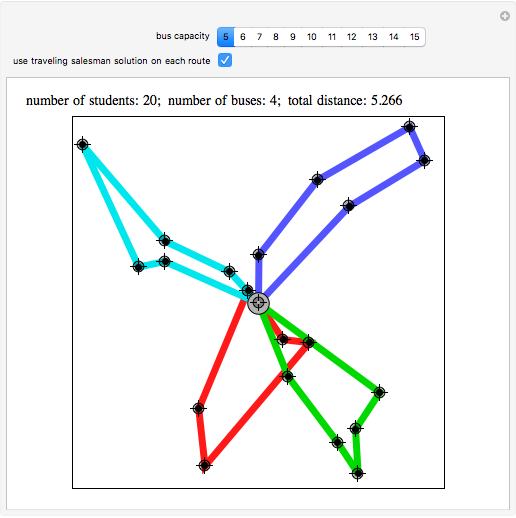
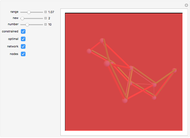
The initial runs are performed without the traveling-salesman post-process step. If such post-processing is requested (as in the second snapshot), it is done on the best run achieved without post-processing. This was done so that you can see the same student partition with and without the post-processing. Another approach, which is only a little slower, is to run a traveling salesman improvement on each of the 11 initial runs and then choose the best. The sweeping method, described in [1], appears to be not as good, but does yield the minimum number of routes.
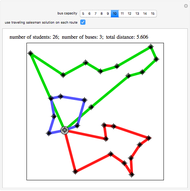
The third snapshot shows that the heuristic is not always optimal, since it is clear that the point on the blue tour that is on the green line could be added to the green tour with a reduction in total cost. One can try post-processing that moves single points around to try to improve the routes, but that is slow and has not been included here.
Reference
[1] G. Gutin, "Traveling Salesman Problems," in Handbook of Graph Theory (J. L. Gross and J. Yellen, eds.), Boca Raton, FL: CRC Press, 2004 pp. 279–299.
Permanent Citation