The Yoshimoto Cube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
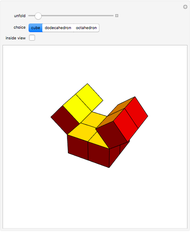
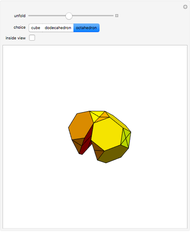
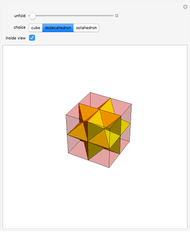
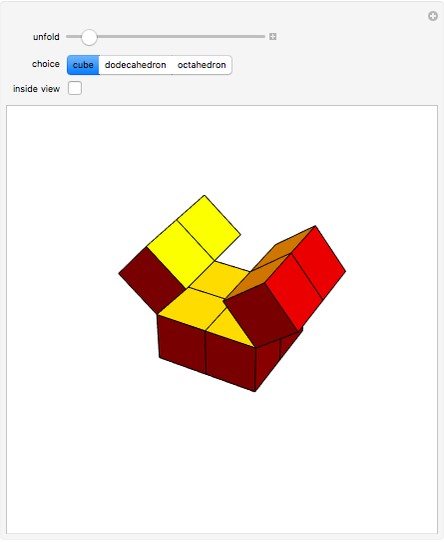
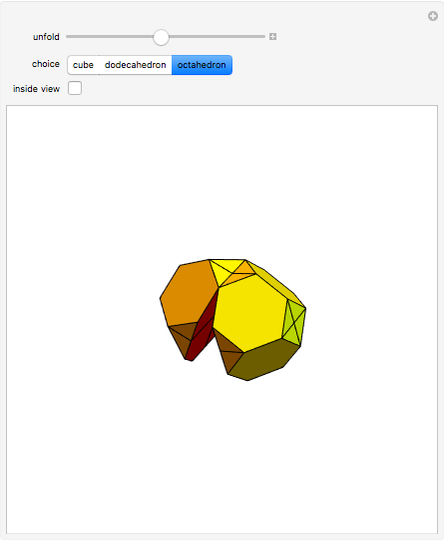
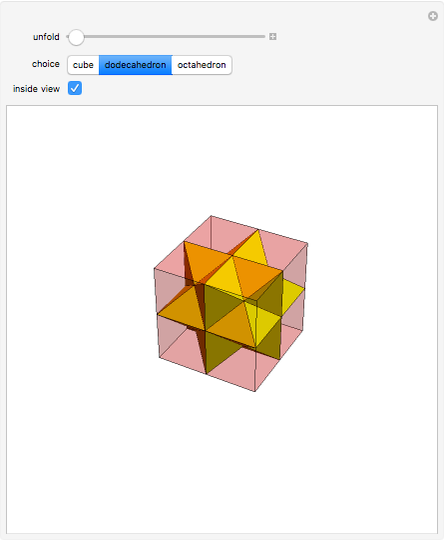
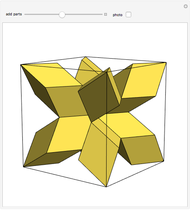
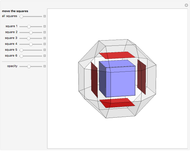
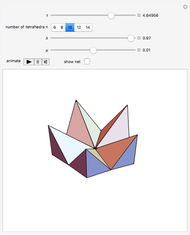
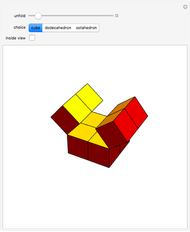
The Yoshimoto cube was invented by the Japanese designer Naoki Yoshimoto in 1971. The cube is made up of eight interconnected cubes and can fold and unfold cyclically. After three steps the eversion shows the cube again but with the initially hidden faces turned to the outside; in three more steps the figure turns back into its original state.
[more]
Contributed by: Hans-Joachim Domke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"The Yoshimoto Cube"
http://demonstrations.wolfram.com/TheYoshimotoCube/
Wolfram Demonstrations Project
Published: March 7 2011