Wolfram Demonstrations Project

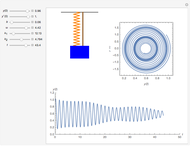
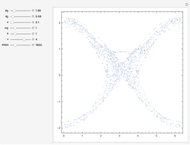
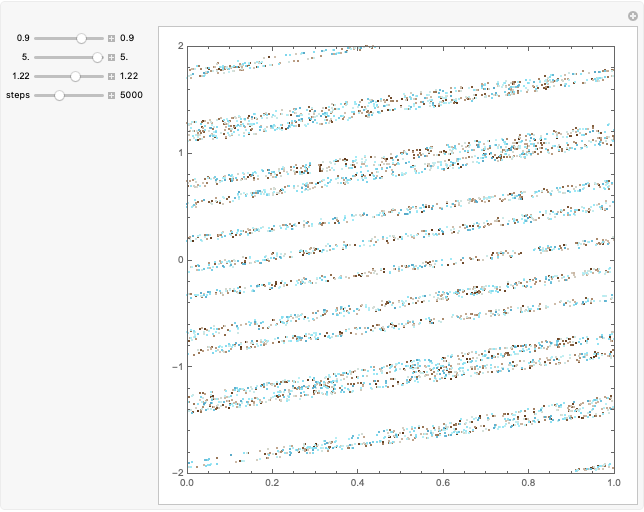
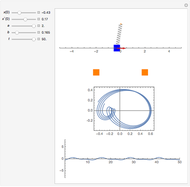
The Zaslavskii map arose from consideration of the problem of a dissipative kicked rotor; it exhibits chaotic behavior. It is claimed to be the simplest problem producing a strange attractor. The approach described involves the so-called action-angle variables of Hamiltonian dynamics (in which frequencies can be obtained without actually solving the equations of motion).

Contributed by: Enrique Zeleny

Slider Zoom
Gamepad Controls
Automatic Animation

Start with the equations of the perturbed system in the variables

and

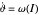where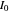

is the action for the stable limit cycle

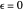(the dimensionless parameter of the perturbation) and

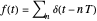is the periodic pulse.

Choosing

integrating between successive pulses, and making the substitutions

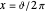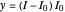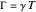the mapping can be rewritten as

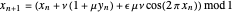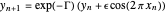with

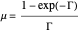References

[1] G. M. Zaslavsky, "The Simplest Case of a Strange Attractor," Physics Letters A, 69(3), 1978 pp. 145–147. doi:10.1016/0375-9601(78)90195-0.

[2] G. Zaslavsky, "Zaslavsky Map," Scholarpedia, 2(5):2662, 2007. doi:10.4249/scholarpedia.2662.

[3] G. Hanchinamani and L. Kulakarni, "Image Encryption Based on 2-D Zaslavskii Chaotic Map and Pseudo Hadmard Transform," International Journal of Hybrid Information Technology, 7(4), 2014 pp. 185–200. www.sersc.org/journals/IJHIT/vol7_no4_ 2014/16.pdf.